Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T14:31:20.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Two remarks on primary spaces

Published online by Cambridge University Press:  07 June 2012

PAUL F. X. MÜLLER
PAUL F. X. MÜLLER*
Affiliation:
Institut für Analysis, J. Kepler Universität, A-4040 Linz, Austria. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for an operator T on ℓ∞(H1 (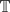)), respectively ℓ∞(L1 (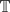)), the identity factors through T or Id - T. Hence ℓ∞(H1 (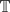)) and ℓ∞(L1 (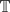)) are primary spaces. We re-prove analogous results of H.M. Wark for the spaces ℓ∞(Hp(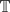)), 1 < p < ∞. In the present paper direct combinatorics of colored dyadic intervals replaces the dependence on Szemerédi's theorem in [11].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 3 , November 2012 , pp. 505 - 523
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Boas, R. P. Jr., Isomorphism between H p and L p. Amer. J. Math. 77 (1955), 655–656.CrossRefGoogle Scholar
[2]Bochkarev, S. V.Construction of polynomial bases in finite-dimensional spaces of functions analytic in the disk. Trudy Mat. Inst. Steklov. 164 (1983), 49–74. Orthogonal series and approximations of functions.Google Scholar
[3]Bourgain, J.On the primarity of H ∞-spaces. Israel J. Math. 45 (4) (1983), 329–336.CrossRefGoogle Scholar
[4]Bourgain, J. and Tzafriri, L.Invertibility of “large” submatrices with applications to the geometry of Banach spaces and harmonic analysis. Israel J. Math. 57 (2) (1987), 137–224.CrossRefGoogle Scholar
[5]Bourgain, J. and Tzafriri, L.Restricted invertibility of matrices and applications. In Analysis at Urbana, Vol. II (Urbana, IL, 1986–1987). London Math. Soc. Lecture Note Ser. vol. 138 (Cambridge University Press, 1989), pp 61–107.Google Scholar
[6]Kwapień, S. and Pełczyński, A.Some linear topological properties of the Hardy spaces H p. Compositio Math. 33 (3) (1976), 261–288.Google Scholar
[7]Maurey, B.Isomorphismes entre espaces H 1. Acta Math. 145 (1–2) (1980), 79–120.CrossRefGoogle Scholar
[8]Müller, P. F. X.On projections in H 1 and BMO. Studia Math. 89 (2) (1988), 145–158.CrossRefGoogle Scholar
[9]Müller, P. F. X.Isomorphisms Between H 1 Spaces. Mathematics Institute of the Polish Academy of Sciences. Mathematical Monographs (New Series). vol. 66 (Birkhäuser Verlag, Basel, 2005).Google Scholar
[10]Szemerédi, E.On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 (1975), 199–245. Collection of articles in memory of Juri Vladimirovic Linnik.CrossRefGoogle Scholar
[11]Wark, H. M.The l ∞ direct sum of L p (1 < p < ∞) is primary. J. Lond. Math. Soc. (2) 75 (1) (2007), 176–186.CrossRefGoogle Scholar
[12]Wojtaszczyk, P.Decompositions of H p spaces. Duke Math. J. 46 (3) (1979), 635–644.CrossRefGoogle Scholar
[13]Wojtaszczyk, P.On projections in spaces of bounded analytic functions with applications. Studia Math. 65 (2) (1979), 147–173.CrossRefGoogle Scholar
[14]Wojtaszczyk, P.Banach Spaces for Analysts. Cambridge Studies in Advanced Math. vol. 25 (Cambridge University Press, 1991).Google Scholar
[15]Zygmund, A.Trigonometric Series. Vol. I, II. Cambridge Mathematical Library (Cambridge University Press, Cambridge, 1988). Reprint of the 1979 edition.Google Scholar