Article contents
Transverse bending of a thin circular plate loaded normally over an eccentric circle
Published online by Cambridge University Press: 24 October 2008
Abstract
Complex variable methods have been applied to isotropic and aelotropic plate problems by several authors. The notation used here is that of Stevenson(14). Dawoud(5) has expressed the continuity conditions between two differently loaded regions in terms of the complex potentials and the particular integrals for the two regions.
The problem of a transverse load at any point of a clamped circular plate was solved by Clebsch(4), Michell(11), Melan(10) and Flügge(6). A series solution for the simply supported circular plate under the same load was given by Foeppel(8). Using Stevenson's tentative method Dawoud(5) applied complex potentials to solve the problem of an eccentric isolated load under certain boundary conditions. Applying Muskhelishvili's method, Washizu(15) obtained the same results for clamped and simply supported boundaries.
It is easy to get solutions for a circular plate concentrically and uniformly loaded. For non-uniform loadings there are the solutions found by Sen (13) for certain distributions of normal thrust over the complete plate or over a concentric circle and the solution of Flügge (7) for a linearly varying load over the simply supported circular plate. The present author and Dawoud(3) obtained the solutions for a circular plate with the load  over the complete plate or over a concentric circle, under a general boundary constraint including as special cases the usual clamped and hinged boundaries. Ghose (9) worked out the problem of a clamped circular plate when the load is uniformly distributed between two concentric circles and two radii. Schmidt (12) found the solution for a clamped circular plate uniformly loaded over an eccentric circle. The complex variable method was applied by the author and Dawoud(2) to obtain the solutions for a circular plate having an eccentric circular patch symmetrically loaded with respect to its centre under the general boundary condition mentioned before. The author (1) also found the solution for a linearly varying load over an eccentric circle under the same boundary condition. In this paper the power of the complex variable method is exhibited by rinding the appropriate complex potentials corresponding to the load
over the complete plate or over a concentric circle, under a general boundary constraint including as special cases the usual clamped and hinged boundaries. Ghose (9) worked out the problem of a clamped circular plate when the load is uniformly distributed between two concentric circles and two radii. Schmidt (12) found the solution for a clamped circular plate uniformly loaded over an eccentric circle. The complex variable method was applied by the author and Dawoud(2) to obtain the solutions for a circular plate having an eccentric circular patch symmetrically loaded with respect to its centre under the general boundary condition mentioned before. The author (1) also found the solution for a linearly varying load over an eccentric circle under the same boundary condition. In this paper the power of the complex variable method is exhibited by rinding the appropriate complex potentials corresponding to the load
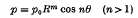
over an eccentric circular patch, where R, θ are measured from the centre of the patch and the common diameter of the plate and the patch. Since the two cases n = 0, 1 require special consideration and were dealt with separately (in (2) and (1) respectively), we see that this paper completes the solution of the problem of a circular plate with an eccentric circular patch symmetrically loaded with respect to the common diameter of the plate and patch, the load being in this case expressible in the form 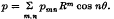 .
.
For a clamped boundary the solution is obtained in finite terms.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 52 , Issue 4 , October 1956 , pp. 742 - 749
- Copyright
- Copyright © Cambridge Philosophical Society 1956
References
REFERENCES
- 2
- Cited by


