Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nicholls, Peter J.
1988.
Holomorphic Functions and Moduli II.
Vol. 11,
Issue. ,
p.
141.
Sheingorn, Mark
2017.
Number Theory with an Emphasis on the Markoff Spectrum.
p.
239.


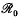 be a Ford fundamental region for Γ in
be a Ford fundamental region for Γ in 