No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let 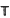 be the circle group, M(
be the circle group, M(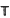 ) the set of bounded Borel measures on
) the set of bounded Borel measures on 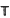 and ℤ the additive group of integers. If μ ∈ M(
and ℤ the additive group of integers. If μ ∈ M(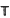 ) and n ∈ ℤ, define
) and n ∈ ℤ, define
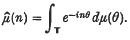
A well-known result of Rajchman states that
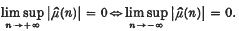
The following quantitative generalization of this result has been given in (2) by K. de Leeuw and Y. Katznelson.