Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cohen, F. R.
May, J. P.
and
Taylor, L. R.
1979.
Splitting of some more spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 2,
p.
227.
Kraines, David
and
Lada, Thomas
1979.
Algebraic Topology Waterloo 1978.
Vol. 741,
Issue. ,
p.
588.
May, J. P.
1979.
Algebraic Topology Waterloo 1978.
Vol. 741,
Issue. ,
p.
625.
May, J. P.
1979.
Algebraic Topology Aarhus 1978.
Vol. 763,
Issue. ,
p.
38.
Eccles, Peter John
1980.
Topology Symposium Siegen 1979.
Vol. 788,
Issue. ,
p.
23.
Eccles, Peter John
1980.
Multiple points of codimension one immersions of oriented manifolds.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 87,
Issue. 2,
p.
213.
Singer, William M.
1981.
A new chain complex for the homology of the Steenrod algebra.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 90,
Issue. 2,
p.
279.
Eccles, Peter John
1981.
Codimension one immersions and the Kervaire invariant one problem.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 90,
Issue. 3,
p.
483.
Steiner, Richard
1982.
Multiplicative transfers in ordinary cohomology.
Proceedings of the Edinburgh Mathematical Society,
Vol. 25,
Issue. 2,
p.
113.
Cohen, F.R.
1984.
Two-primary analogues of Selick's theorem and the Kahn-Priddy theorem for the 3-sphere.
Topology,
Vol. 23,
Issue. 4,
p.
401.
Lannes, J.
1984.
Algebraic Topology Aarhus 1982.
Vol. 1051,
Issue. ,
p.
263.
FUKAGAWA, Hisashi
1984.
Equivariant transfer for finite G-coverings.
Japanese journal of mathematics. New series,
Vol. 10,
Issue. 1,
p.
117.
Gray, Brayton
1984.
Unstable families related to the image of J.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 96,
Issue. 1,
p.
95.
Kuhn, Nicholas J.
and
Priddy, Stewart B.
1985.
The transfer and Whitehead's conjecture.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 98,
Issue. 3,
p.
459.
Cohen, R. L.
Jones, J. D. S.
and
Mahowald, M. E.
1985.
The Kervaire invariant of immersions.
Inventiones Mathematicae,
Vol. 79,
Issue. 1,
p.
95.
1986.
Vol. 121,
Issue. ,
p.
395.
Bödigheimer, C.-F.
1987.
Algebraic Topology.
Vol. 1286,
Issue. ,
p.
174.
Cohen, F. R.
1987.
Algebraic Topology.
Vol. 1286,
Issue. ,
p.
1.
Kuhn, Nicholas J.
1987.
The transfer and James-Hopf invariants.
Mathematische Zeitschrift,
Vol. 196,
Issue. 3,
p.
391.
Barratt, M. G.
Jones, J. D. S.
and
Mahowald, M. E.
1987.
Algebraic Topology.
Vol. 1286,
Issue. ,
p.
135.


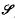
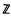 , denote the components of
, denote the components of 