Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T08:36:20.161Z Has data issue: false hasContentIssue false
  • English
  • Français

Torsion of beams whose cross-section is a regular polygon of n sides

Published online by Cambridge University Press:  24 October 2008

B. R. Seth
Get access Rights & Permissions [Opens in a new window]

Extract

E. Trefftz has discussed the problem of the torsion of a beam whose cross-section is bounded by a polygon with the help of the Schwarz-Christoffel transformation given by

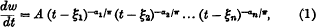
where a1, a2, …, an are external angles of the polygon in the w-plane, and ξ1, ξ2, …, ξn are the points on the real ξ-axis in the t-plane that correspond to the angular points of the polygon in the w-plane. In the case of regular polygons a further transformation of the upper half of the t-plane into the interior of a circle in the z-plane with the help of the transformation

greatly simplifies the problem, and some definite results can be obtained.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 30 , Issue 2 , 30 April 1934 , pp. 139 - 149
Copyright
Copyright © Cambridge Philosophical Society 1934

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Math. Ann. 82 (1921), 306–319.Google Scholar

* This result is due to Schwarz. See Forsyth, , Theory of functions, 3rd edition, p. 768, Ex. 2.Google Scholar

* Cf. Dixon, A. C., Quart. Journ. of Math. 24 (1890), 167–233.Google Scholar

* Richelot, , Journal für Math. 9 (1832), 407–408Google Scholar, also Cayley, , Proc. Camb. Phil. Soc. 4 (1881), 106–109.Google Scholar

* Thomson, and Tait, , Natural Philosophy, Vol. i, Part 2, pp. 249–250.Google Scholar

* That this supposition of Boussinesq is not always true has been shown by Filon, L. N. G., Phil. Trans. Roy. Soc. 193 (1900), 309–352.CrossRefGoogle Scholar