Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T14:45:29.092Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric energy-momentum tensors in relativistic field theories

Published online by Cambridge University Press:  24 October 2008

J. S. de Wet
J. S. de Wet
Affiliation:
Balliol CollegeOxford
Get access Rights & Permissions [Opens in a new window]

Extract

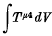In relativistic field theories derived by a variation principle from a Lagrangian, the problem arises of finding a symmetric tensor of rank 2 which has vanishing divergence in virtue of the field equations and is such that taken over a space-like section is equal to the corresponding integral of the so-called canonical energy-momentum tensor. It is well known that the latter condition is satisfied if the difference between the two tensors is the divergence of an antisymmetric tensor of rank 3.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 43 , Issue 4 , October 1947 , pp. 511 - 520
Copyright
Copyright © Cambridge Philosophical Society 1947

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Born, . Ann. Inst. Poincaré, 7 (1937), 155.Google Scholar
(2)Belinfante, . Physica, 6 (1939), 887.CrossRefGoogle Scholar
(See also Pauli, , Rev. Mod. Phys. 13 (1941), 203.)CrossRefGoogle Scholar
(3) Podolsky and Kikuchi, . Phys. Rev. 65 (1944), 228.Google Scholar
(4)Chang, . Proc. Cambridge Phil. Soc. 42 (1946), 132.CrossRefGoogle Scholar