Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T04:04:20.417Z Has data issue: false hasContentIssue false
  • English
  • Français

Surjectivity of the Taylor map for complex nilpotent Lie groups

Published online by Cambridge University Press:  01 January 2009

BRUCE K. DRIVER ,
LEONARD GROSS  and
LAURENT SALOFF-COSTE
BRUCE K. DRIVER
Affiliation:
Department of Mathematics, 0112University of California, San Diego, La Jolla, CA 92093-0112, U.S.A. e-mail: [email protected]
LEONARD GROSS
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853-4201, U.S.A. e-mail: [email protected], [email protected]
LAURENT SALOFF-COSTE
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853-4201, U.S.A. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Hermitian form q on the dual space, 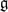*, of the Lie algebra, 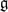, of a simply connected complex Lie group, G, determines a sub-Laplacian, Δ, on G. Assuming Hörmander's condition for hypoellipticity, there is a smooth heat kernel measure, ρt, on G associated to etΔ/4. In a companion paper [6], we proved the existence of a unitary “Taylor” map from the space of holomorphic functions in L2(G, ρt) onto Jt0 (a subspace of) the dual of the universal enveloping algebra of 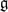. Here we give a very different proof of the surjectivity of the Taylor map under the assumption that G is nilpotent. This proof provides further insight into the structure of the Taylor map. In particular we show that the finite rank tensors are dense in Jt0 when the Lie algebra is graded and the Laplacian is adapted to the gradation. We also show how the Fourier–Wigner transform produces a natural family of holomorphic functions in L2(G, ρt), for appropriate t, when G is the complex Heisenberg group.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 146 , Issue 1 , January 2009 , pp. 177 - 195
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bourbaki, N.Éléments de mathématique. Fasc. XXXVII. Groupes et algèbres de Lie. Chapitre II: Algèbres de Lie libres. Chapitre III: Groupes de Lie (Hermann, 1972). Actualités Scientifiques et Industrielles, No. 1349.Google Scholar
[2]Cook, J. M.The mathematics of second quantization. Trans. Amer. Math. Soc. 74: (1953), 222–245.CrossRefGoogle Scholar
[3]Courant, R. and Hilbert, D.Methods of Mathematical Physics. Vol. I (Interscience Publishers, 1953).Google Scholar
[4]Driver, B. K.On the Kakutani–Itô–Segal–Gross and Segal–Bargmann–Hall isomorphisms. J. Funct. Anal. 133 (1): (1995) 69–128.CrossRefGoogle Scholar
[5]Driver, B. K. and Gross, L. Hilbert spaces of holomorphic functions on complex Lie groups. In New trends in stochastic analysis (Charingworth, 1994), pages 76–106. (World Scientific Publishing, 1997).Google Scholar
[6]Driver, B. K., Gross, L. and Saloff-Coste, L. Holomorphic functions and subelliptic heat kernels over lie groups. To appear in the Journal of the European Mathematical Society.Google Scholar
[7]Folland, G. B. and Stein, E. M.Hardy spaces on homogeneous groups. Mathematical Notes. vol. 28 (Princeton University Press, 1982).Google Scholar
[8]Folland, G. B. Harmonic analysis in phase space, Annals of Mathematics Studies vol. 122 (Princeton University Press, 1989).CrossRefGoogle Scholar
[9]Goodman, R. W.Nilpotent Lie groups: structure and applications to analysis. Lecture Notes in Mathematics, vol. 562 (Springer-Verlag, 1976).CrossRefGoogle Scholar
[10]Gorbatsevich, V. V., Onishchik, A. L. and Vinberg, E. B.Foundations of Lie Theory and Lie Transformation Groups (Springer-Verlag, 1997). Translated from the Russian by A. Kozlowski, Reprint of the 1993 translation [Lie groups and Lie algebras. I, Encyclopaedia Math. Sci. 20 (Springer, 1993), MR1306737 (95f:22001)].Google Scholar
[11]Gottfried, K. Quantum mechanics: fundamentals. Cambridge Tracts in Mathematics vol. 1 (Benjamin, first edition, 1966).Google Scholar
[12]Gross, L.Analytic vectors for representations of the canonical commutation relations and nondegeneracy of ground states. J. Funct. Anal. 17 (1974), 104–111.CrossRefGoogle Scholar
[13]Gross, L.Logarithmic Sobolev inequalities. Amer. J. Math. 97 (4) (1975), 1061–1083.CrossRefGoogle Scholar
[14]Gross, L.Some norms on universal enveloping algebras. Canad. J. Math. 50 (2) (1998), 356–377.CrossRefGoogle Scholar
[15]Gross, L.A local Peter–Weyl theorem. Trans. Amer. Math. Soc. 352 (1) (2000), 413–427.CrossRefGoogle Scholar
[16]Hörmander, L.Hypoelliptic second order differential equations. Acta Math. 119 (1967), 147–171.CrossRefGoogle Scholar
[17]Jacobi, C. G. J.Zur theorie der variations-rechnung und der differential-gleichungen. J. Reine Angew. Math. von Crelle 17 (1837), 68–82.Google Scholar
[18]Jerison, D. and Sánchez–Calle, A. Subelliptic, second order differential operators. In Complex analysis, III (College Park, Md., 1985–86), Lecture Notes in Math. vol. 1277, pages 46–77 (Springer, 1987).CrossRefGoogle Scholar
[19]Krötz, B., Thangavelu, S. and Xu, Y.The heat kernel transform for the Heisenberg group. J. Funct. Anal. 225 (2) (2005), 301–336.CrossRefGoogle Scholar
[20]Nelson, E.Analytic vectors. Ann. of Math. (2) 70 (1959), 572–615.CrossRefGoogle Scholar
[21]Reed, M. and Simon, B.Methods of Modern Mathematical Physics. II. Fourier analysis, Self-Adjointness (Academic Press [Harcourt Brace Jovanovich Publishers], 1975).Google Scholar
[22]Reed, M. and Simon, B.Methods of Modern Mathematical Physics. I. (Academic Press Inc. [Harcourt Brace Jovanovich Publishers], second edition, 1980). Functional analysis.Google Scholar
[23]Rothschild, L. P. and Stein, E. M.Hypoelliptic differential operators and nilpotent groups. Acta Math. 137 (3–4) (1976), 247–320.CrossRefGoogle Scholar
[24]Simon, B.Functional Integration and Quantum Physics (AMS Chelsea Publishing, second edition, 2005).CrossRefGoogle Scholar
[25]Titchmarsh, E. C.The Theory of Functions (Oxford University Press, 2nd edition, 1968).Google Scholar
[26]Varadarajan, V. S.Lie groups, Lie algebras, and their representations. Graduate Texts in Mathematics vol. 102 (Springer-Verlag, 1984). Reprint of the 1974 edition.CrossRefGoogle Scholar
[27]Varopoulos, N. Th., Saloff-Coste, L. and Coulhon, T.Analysis and Geometry on Groups. (Cambridge University Press, 1992).Google Scholar