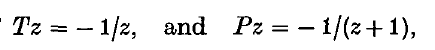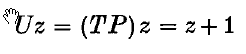Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stothers, W. W.
1977.
The number of subgroups of given index in the modular group.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 78,
Issue. 1-2,
p.
105.
Patterson, S. J.
1977.
Ramified coverings of Riemann surfaces.
Archiv der Mathematik,
Vol. 28,
Issue. 1,
p.
281.
Stothers, W. Wilson
1977.
Subgroups of the (2,3,7) triangle group.
manuscripta mathematica,
Vol. 20,
Issue. 4,
p.
323.
Stothers, W. W.
1978.
Subgroups of infinite index in the modular group.
Glasgow Mathematical Journal,
Vol. 19,
Issue. 1,
p.
33.
Merzlyakov, Yu. I.
1980.
Linear groups.
Journal of Soviet Mathematics,
Vol. 14,
Issue. 1,
p.
887.
Stothers, W. W.
1981.
Subgroups of infinite index in the modular group III.
Glasgow Mathematical Journal,
Vol. 22,
Issue. 2,
p.
119.
Brenner, J.L.
and
Lyndon, R.C.
1983.
The Orbits of the Product of Two Permutations.
European Journal of Combinatorics,
Vol. 4,
Issue. 4,
p.
279.
Brenner, J. L.
and
Lyndon, R. C.
1983.
Maximal nonparabolic subgroups of the modular group.
Mathematische Annalen,
Vol. 263,
Issue. 1,
p.
1.
Stothers, W. W.
1984.
Level and index in the modular group.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 99,
Issue. 1-2,
p.
115.
Lyndon, R. C.
1984.
Groups — Korea 1983.
Vol. 1098,
Issue. ,
p.
69.
Venkov, A. B.
1989.
Examples of effective solution of the Riemann-Hilbert problem on construction of a differential equation from the monodromy group in the framework of the theory of automorphic functions.
Journal of Soviet Mathematics,
Vol. 46,
Issue. 2,
p.
1707.
Jones, Gareth A.
2020.
Galois Covers, Grothendieck-Teichmüller Theory and Dessins d'Enfants.
Vol. 330,
Issue. ,
p.
121.
Alolaiyan, Hanan
Razaq, Abdul
Yousaf, Awais
Zahra, Rida
and
Yildirim, Kenan
2021.
A Comprehensive Overview on the Formation of Homomorphic Copies in Coset Graphs for the Modular Group.
Journal of Mathematics,
Vol. 2021,
Issue. ,
p.
1.
Aamir, Muhammad
Yousaf, Awais
Masmali, Ibtisam
Razaq, Abdul
and
Luciano, Gaetano
2023.
Number of Distinct Fragments in Coset Diagrams for
P
S
L
2
,
Z
.
Journal of Mathematics,
Vol. 2023,
Issue. ,
p.
1.
Tiwari, Devendra
and
Reddy, Harshavardhan
2025.
Geometry, Groups and Mathematical Philosophy.
Vol. 811,
Issue. ,
p.
241.