Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Duan, Z. Y.
1992.
The structure of noetherian modules over hyperfinite groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 112,
Issue. 1,
p.
21.
Duan, Z. Y.
and
Tomkinson, M. J.
1993.
The decomposition of minimax modules over hyperfinite groups.
Archiv der Mathematik,
Vol. 61,
Issue. 4,
p.
340.
Qin, Y. B.
1996.
The decomposition of artinian modules over hyper-(cyclic or finite) groups.
Proceedings of the Edinburgh Mathematical Society,
Vol. 39,
Issue. 1,
p.
115.


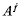 each of whose irreducible ℤZ;
each of whose irreducible ℤZ;