Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T07:37:57.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Splitting ℂP∞ and Bℤ/pn into Thom spectra

Published online by Cambridge University Press:  28 June 2011

Brayton Gray  and
Nigel Ray
Brayton Gray
Affiliation:
University of Illinois at Chicago, Box 4348, Chicago IL 60680, U.S.A.
Nigel Ray
Affiliation:
The University, Manchester M13 9PL, England
Get access Rights & Permissions [Opens in a new window]

Extract

In recent years, much work in algebraic topology has been devoted to stable splitting phenomena. Often the existence of these splittings has first been detected at the cohomological level in terms of modules over the Steenrod algebra.

For example, W. Richter has exhibited a decomposition of ΩSU(n) of the form

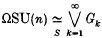
(see [7]). Not only were cohomology calculations the initial evidence for this situation, but they further suggested that each summand Gk might be the Thom complex of a suitable k-plane complex vector bundle. This possibility was also verified by Mitchell.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 106 , Issue 2 , September 1989 , pp. 263 - 271
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bousfield, A. K. and Kan, D. M.. Homotopy Limits, Completions and Localizations. Lecture Notes in Math. vol. 304 (Springer-Verlag, 1972).CrossRefGoogle Scholar
[2] Harris, J. C. and Kuhn, N. J.. Stable decompositions of classifying spaces of finite abelian p-groups. Math. Proc. Cambridge Philos. Soc. 103 (1988), 427–449.CrossRefGoogle Scholar
[3] Holszager, R.. Stable splittings of K(G, 1). Proc. Amer. Math. Soc. 31 (1972), 305–306.Google Scholar
[4] May, J. P.. Classifying Spaces and Fibrations. Mem. Amer. Math. Soc. no. 155 (American Mathematical Society, 1975).CrossRefGoogle Scholar
[5] Milgram, R. J.. The bar construction and abelian H-spaces. Illinois J. Math. 11 (1967), 242–250.Google Scholar
[6] Miller, H.. Stable splitting of Stiefel manifolds. Topology 24 (1985), 411–419.CrossRefGoogle Scholar
[7] Mitchell, S. A.. A filtration of the loops on SU(n) by Schubert varieties. Math. Z. 193 (1986), 347–362.CrossRefGoogle Scholar
[8] Mitchell, S. A. and Priddy, S. B.. Stable splittings derived from the Steinberg module. Topology 22 (1983), 285–298.CrossRefGoogle Scholar
[9] Roush, F. W.. Transfer in generalised cohomology theories. Ph.D. thesis, Princeton University (1971).Google Scholar
[10] Steenrod, N. E.. Milgram's classifying space of a topological group. Topology 7 (1968), 349–368.CrossRefGoogle Scholar
[11] Sullivan, D.. Genetics of homotopy theory and the Adams conjecture. Ann. of Math. (2) 100 (1974), 1–79.CrossRefGoogle Scholar