Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-27T04:45:03.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Spinors in Hilbert space

Published online by Cambridge University Press:  24 October 2008

R. J. Plymen
R. J. Plymen
Affiliation:
University of Manchester
Get access Rights & Permissions [Opens in a new window]

Extract

In 1913, É. Cartan discovered that the special orthogonal group SO(k) has a ‘two-valued’ representation (i.e. a projective representation) on a complex vector space S of dimension 2n, where k = 2n or 2n + 1. The projective representation in question lifts to a true representation of the double cover Spin (k) of SO(k). We restrict attention to the case k = 2n. Under the action of Spin (2n), S breaks up into 2 irreducible subspaces:

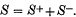
The vectors in S are called spinors (relative to SO(2n)), those in S+ or S− are called half-spinors (4).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 2 , September 1976 , pp. 337 - 347
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Atiyah, M. F., Bott, R. and Shapiro, A.Clifford modules. Topology 3, suppl. 1 (1964), 3–38. Reprinted in (3).Google Scholar
(2)Bongaarts, P. J. M. Linear fields according to I. E. Segal. Mathematics of contemporary physics, ed. Streater, R. F. (London, Academic Press, 1972).Google Scholar
(3)Bott, R.Lectures on K(X) (New York, Benjamin, 1969).Google Scholar
(4)Chevalley, C.The algebraic theory of spinors (New York, Columbia University Press, 1954).Google Scholar
(5)De La Harpe, P.The Clifford algebra and the spinor group of a Hilbert space. Compositio Math. 25 (1972), 245–261.Google Scholar
(6)Hitchin, N.Harmonic spinors. Advances in Math. 14 (1974), 1–55.CrossRefGoogle Scholar
(7)Hugenholtz, N. M. and Kadison, R. V.Automorphisme and quasi-free states of the CAR algebra. Comm. Math. Phys. 43 (1975), 181–197.Google Scholar
(8)Mackey, G.Mathematical foundations of quantum mechanics (New York, Benjamin, 1963).Google Scholar
(9)Shale, D. and Stinespring, W. F.Spinor representations of infinite orthogonal groups. J. Math. Mech. 14 (1965), 315–322.Google Scholar
(10)Streater, R. F.The Heisenberg ferromagnet as a quantum field theory. Comm. Math. Phys. 6 (1967), 233–247.Google Scholar
(11)Schrader, R. and Uhlenbrock, D. A.Markov structures on Clifford algebras. J. Functional Analysis 18 (1975), 369–413.Google Scholar
(12)Dirac, P. A. M.Spinors in Hilbert space (Centre for Theoretical Studies, University of Miami, Coral Gables, Florida 3 3124, 1970).Google Scholar