No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
1. In a paper published recently in these Proceedings, I have proved the formulae
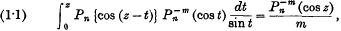
where R(m)>0;
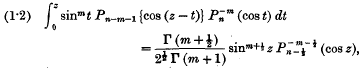
where R(m) > −½; and
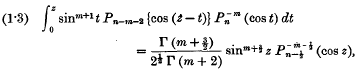
where R(m) >− 1. In each case n is unrestricted.