Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hayman, W. K.
1948.
Some inequalities in the theory of functions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 44,
Issue. 2,
p.
159.
Hayman, W. K.
1951.
The maximum modulus and valency of functions meromorphic in the unit circle.
Acta Mathematica,
Vol. 86,
Issue. 0,
p.
89.
Hayman, W. K.
1951.
The maximum modulus and valency of functions meromorphic in the unit circle.
Acta Mathematica,
Vol. 86,
Issue. 0,
p.
193.
Jenkins, J. A.
1955.
On Explicit Bounds In Schottky's Theorem.
Canadian Journal of Mathematics,
Vol. 7,
Issue. ,
p.
76.
Jenkins, J. A.
1956.
On Explicit Bounds In Landau's Theorem.
Canadian Journal of Mathematics,
Vol. 8,
Issue. ,
p.
423.
Hersch, Joseph
1956.
Contribution à la théorie des fonctions pseudo-analytiques.
Commentarii Mathematici Helvetici,
Vol. 30,
Issue. 1,
p.
1.
Chiang, P. S.
1969.
Computer investigation of Landau’s theorem.
Mathematics of Computation,
Vol. 23,
Issue. 105,
p.
185.
1973.
Introduction to the Theory of Entire Functions.
Vol. 56,
Issue. ,
p.
186.
Hayman, W. K.
1977.
Complex Analysis.
Vol. 599,
Issue. ,
p.
68.
1979.
An Introduction to Classical Complex Analysis.
Vol. 82,
Issue. ,
p.
462.
Pommerenke, Ch.
1979.
On the growth of normal analytic functions.
Journal d'Analyse Mathématique,
Vol. 36,
Issue. 1,
p.
227.
Gehring, F. W.
and
Pommerenke, Ch.
1984.
On the Nehari univalence criterion and quasicircles.
Commentarii Mathematici Helvetici,
Vol. 59,
Issue. 1,
p.
226.
1989.
Subharmonic Functions.
p.
865.
Zhang, Shunyab
1990.
On explicit bounds in schottky's theorem.
Complex Variables, Theory and Application: An International Journal,
Vol. 13,
Issue. 3-4,
p.
161.
Rupp, Rudolf
1994.
A covering theorem for a composite class of analytic functions.
Complex Variables, Theory and Application: An International Journal,
Vol. 25,
Issue. 1,
p.
35.
Qiu, S.-L
and
Vuorinen, M.
1996.
Quasimultiplicative properties for the η-distortion function.
Complex Variables, Theory and Application: An International Journal,
Vol. 30,
Issue. 1,
p.
77.
Qiu, Songliang
1997.
Agard’s η-distortion function and Schottky’s theorem.
Science in China Series A: Mathematics,
Vol. 40,
Issue. 1,
p.
1.
Li, Zhong
and
Qi, Yi
2007.
A remark on Schottky's theorem.
Bulletin of the London Mathematical Society,
Vol. 39,
Issue. 2,
p.
242.
Batra, Prashant
2007.
On Gol’dberg’s Constant A2.
Computational Methods and Function Theory,
Vol. 7,
Issue. 1,
p.
33.
2008.
Nine Introductions in Complex Analysis.
Vol. 208,
Issue. ,
p.
473.


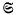 the class of all functions regular in |
the class of all functions regular in |