Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T08:34:52.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Some numerical results on the characters of exceptional Weyl groups

Published online by Cambridge University Press:  24 October 2008

W. M. Beynon  and
G. Lusztig
W. M. Beynon
Affiliation:
University of Warwick, Coventry
G. Lusztig
Affiliation:
Mathematics Institute, University of Warwick, and M.I.T
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let V be an l-dimensional real vector space and let W be a finite subgroup of GL(V) generated by reflexions such that the space of W-invariant vectors in V is zero. Then W acts naturally on the symmetric algebra S of V preserving the natural grading 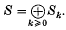. LetI be the ideal in S generated by the w-invariant elements in 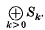. The quotient algebra 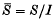inherits the W-action and also a grading

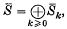
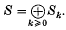is the image of Sk under S → S̅. It is well known that the W-module S̅ is isomorphic to the regular representation of W (see (3), ch. v, 5·2); in particular, S̅k = 0 for large k. (More precisely, S̅k = 0 for k > ν, where ν is the number of reflexions in W.)If ρ is an irreducible character of W, we denote by nk(ρ) the multiplicity of ρ in the W- module S̅k. The sequence n(ρ) = (n0(ρ), n1(ρ), n2(ρ), …) is an interesting invariant of the character ρ For example, in the study of unipotent classes in semisimple groups, one encounters the following question: what is the smallest k for which nk(ρ) 4= 0 (with ρ as above) and, then, what is nk(ρ) Also, the polynomial in q

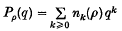
can sometimes be interpreted as the dimension of an irreducible representation of a Chevalley group over the field with q elements. For these reasons it seems desirable to describe explicitly the sequence n(ρ) (or, equivalently, the polynomial Pρ(q)) for the various irreducible characters ρ of W. When W is a Weyl group of type Al, this is contained in the work of Steinberg (8); in the case where W is a Weyl group of type Bl or Dl this is done in (7),§2.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 84 , Issue 3 , November 1978 , pp. 417 - 426
Copyright
Copyright © Cambridge Philosophical Society 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Referencess

(1)Benson, C. T. and Curtis, C. W.On the degrees and rationality of certain characters of finite Chevalley groups. Trans. Amer. Math. Soc. 165 (1972), 251–273.CrossRefGoogle Scholar
(2)Benson, C. T. and Curtis, C. W.Corrections and additions to (1). Trans. Amer. Math. Soc. 202 (1972), 405–406.Google Scholar
(3)Bourbaki, N.Groupes et algèbres de Lie (Paris, Hermann, 1968), chs. 4–6.Google Scholar
(4)Frame, J. S.The classes and representations of the groups of 27 lines and 28 bitangents. Ann. Mat. Pura. Appl. (4) 32 (1951), 83–119.CrossRefGoogle Scholar
(5)Frame, J. S. The characters of the Weyl group E 8. Computational problems in abstract algebra (Oxford conference, 1967), ed. Leech, J., 111–130.Google Scholar
(6)Knuth, D. E.The art of computer programming (Addison-Wesley, 1975).Google Scholar
(7)Lusztig, G.Irreducible representations of finite classical groups. Inventiones Math. 43 (1977), 125–175.CrossRefGoogle Scholar
(8)Steinberg, R.A geometric approach to the representations of the full linear group over a Galois field. Trans. Amer. Math. Soc. 71 (1951), 274–282.CrossRefGoogle Scholar