Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kalton, N. J.
1971.
Subseries convergence in topological groups and vector spaces.
Israel Journal of Mathematics,
Vol. 10,
Issue. 4,
p.
402.
Horváth, John
1973.
Summer School on Topological Vector Spaces.
Vol. 331,
Issue. ,
p.
41.
Kalton, N. J.
1973.
On summability domains.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 73,
Issue. 2,
p.
327.
Eberhardt, Volker
1974.
�ber einen Graphensatz f�r Abbildungen mit normiertem Zielraum.
Manuscripta Mathematica,
Vol. 12,
Issue. 1,
p.
47.
Tweddle, I.
1975.
Some results involving weak compactness in C(X), C(υX) and C(X)′.
Proceedings of the Edinburgh Mathematical Society,
Vol. 19,
Issue. 3,
p.
221.
Pfister, Helmut
1975.
Zwei Bemerkungen �ber (DF)-R�ume.
Archiv der Mathematik,
Vol. 26,
Issue. 1,
p.
646.
Drewnowski, L.
1975.
The metrizable linear extensions of metrizable sets in topological linear spaces.
Proceedings of the American Mathematical Society,
Vol. 51,
Issue. 2,
p.
323.
Popoola, J. O.
and
Tweddle, I.
1976.
On the closed graph theorem.
Glasgow Mathematical Journal,
Vol. 17,
Issue. 2,
p.
89.
Bellenot, Steven F.
and
Ostling, Edward G.
1977.
Completeness and intertwined completeness of locally convex spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 81,
Issue. 1,
p.
25.
Popoola, J. O.
and
Tweddle, I.
1977.
A variant of separability in dual systems.
Proceedings of the Edinburgh Mathematical Society,
Vol. 20,
Issue. 4,
p.
317.
Dierolf, Peter
1977.
Theorems of the Orlicz-Pettis-type for locally convex spaces.
Manuscripta Mathematica,
Vol. 20,
Issue. 1,
p.
73.
Pfister, Helmut
1977.
�ber das Gewicht und den �berdeckungstyp von uniformen R�umen und einige Formen des Satzes von Banach-Steinhaus.
Manuscripta Mathematica,
Vol. 20,
Issue. 1,
p.
51.
Pfister, Helmut
1977.
A new characterization of barrelled spaces.
Proceedings of the American Mathematical Society,
Vol. 65,
Issue. 1,
p.
103.
Marquina, Antonio
1977.
A note on the closed graph theorem.
Archiv der Mathematik,
Vol. 28,
Issue. 1,
p.
82.
Dierolf, Peter
and
Dierolf, Susanne
1978.
On linear topologies determined by a family of subsets of a topological vector space.
General Topology and its Applications,
Vol. 8,
Issue. 2,
p.
127.
1978.
Saks Spaces and Applications to Functional Analysis.
Vol. 28,
Issue. ,
p.
1.
Saiflu, H.
and
Tweddle, I.
1980.
The domain spaces for Marquina's closed graph theorem.
Archiv der Mathematik,
Vol. 34,
Issue. 1,
p.
463.
Saiflu, H.
and
Tweddle, I.
1980.
From B-completeness to countable codimensional subspaces via the closed graph theorem.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 86,
Issue. 1-2,
p.
107.
1982.
Topics in Locally Convex Spaces.
Vol. 67,
Issue. ,
p.
501.
Oberguggenberger, Michael
1986.
Über Folgenkonvergenz in lokalkonvexen Räumen.
Mathematische Nachrichten,
Vol. 129,
Issue. 1,
p.
219.
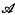 is a particular class of locally convex spaces then ℒ(
is a particular class of locally convex spaces then ℒ(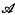 ) is the class of all E such that (E, F)∈ℒ for all F ∈
) is the class of all E such that (E, F)∈ℒ for all F ∈ 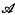 .
.

