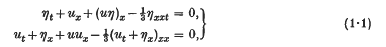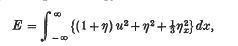Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Toland, J. F.
1983.
Systems of Nonlinear Partial Differential Equations.
p.
373.
Amick, C. J.
and
Toland, J. F.
1983.
Nonlinear elliptic eigenvalue problems on an infinite strip ? Global theory of bifurcation and asymptotic bifurcation.
Mathematische Annalen,
Vol. 262,
Issue. 3,
p.
313.
Toland, J. F.
1984.
Uniqueness and a priori bounds for certain homoclinic orbits of a Boussinesq system modelling solitary water waves.
Communications in Mathematical Physics,
Vol. 94,
Issue. 2,
p.
239.
Hofer, Helmut
and
Toland, John
1984.
Homoclinic, heteroclinic, and periodic orbits for a class of indefinite Hamiltonian systems.
Mathematische Annalen,
Vol. 268,
Issue. 3,
p.
387.
Toland, J. F.
1984.
Positive solutions of nonlinear elliptic equations—existence and nonexistence of solutions with radial symmetry in 𝐿_{𝑝}(𝑅^{𝑁}).
Transactions of the American Mathematical Society,
Vol. 282,
Issue. 1,
p.
335.
Peletier, Mark A
1999.
Non-existence and uniqueness results for fourth-order Hamiltonian systems.
Nonlinearity,
Vol. 12,
Issue. 6,
p.
1555.
Bridges, Thomas J.
and
Derks, Gianne
1999.
Unstable eigenvalues and the linearization about solitary waves and fronts with symmetry.
Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 455,
Issue. 1987,
p.
2427.
Chen, Min
2000.
Solitary-wave and multi-pulsed traveling-wave solutions of boussinesq systems.
Applicable Analysis,
Vol. 75,
Issue. 1-2,
p.
213.
Pelloni, Beatrice
and
Dougalis, Vassilios A.
2001.
Numerical modelling of two-way propagation of non-linear dispersive waves.
Mathematics and Computers in Simulation,
Vol. 55,
Issue. 4-6,
p.
595.
Beardmore, R. E.
Peletier, M. A.
Budd, C. J.
and
Wadee, M. Ahmer
2005.
Bifurcations of Periodic Solutions Satisfying the Zero-Hamiltonian Constraint in Reversible Differential Equations.
SIAM Journal on Mathematical Analysis,
Vol. 36,
Issue. 5,
p.
1461.
Dougalis, V. A.
Durán, A.
López-Marcos, M. A.
and
Mitsotakis, D. E.
2007.
A Numerical Study of the Stability of Solitary Waves of the Bona–Smith Family of Boussinesq Systems.
Journal of Nonlinear Science,
Vol. 17,
Issue. 6,
p.
569.
Antonopoulos, D.C.
Dougalis, V.A.
and
Mitsotakis, D.E.
2010.
Numerical solution of Boussinesq systems of the Bona–Smith family.
Applied Numerical Mathematics,
Vol. 60,
Issue. 4,
p.
314.
Bao, Ellen ShiTing
Chen, Robin Ming
and
Liu, Qing
2015.
Existence and Symmetry of Ground States to the Boussinesq abcd Systems.
Archive for Rational Mechanics and Analysis,
Vol. 216,
Issue. 2,
p.
569.
Motsepa, Tanki
and
Khalique, Chaudry Masood
2018.
A study of the Bona-Smith system describing the two-way propagation of water waves in a channel.
Vol. 1978,
Issue. ,
p.
210002.
Chen, Robin Ming
and
Jin, Jie
2022.
Global bifurcation of solitary waves to the Boussinesq abcd system.
Journal of Differential Equations,
Vol. 310,
Issue. ,
p.
235.