Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-03T01:58:46.326Z Has data issue: false hasContentIssue false
  • English
  • Français

The smallest subgroup whose invariants are hit by the Steenrod algebra

Published online by Cambridge University Press:  12 February 2007

NGUYỄN H. V. HƯNG  and
TRAN DINH LUONG
NGUYỄN H. V. HƯNG
Affiliation:
Department of Mathematics, Vietnam National University, Hanoi 334 Nguyễn Trãi Street, Hanoi, Vietnam. e-mail: [email protected]
TRAN DINH LUONG
Affiliation:
Department of Mathematics, Quynhon University, 170 An Duong Vuong Street, Quynhon, Vietnam. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let V be a k-dimensional 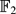-vector space and let W be an n-dimensional vector subspace of V. Denote by GL(n, 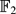) • 1k-n the subgroup of GL(V) consisting of all isomorphisms ϕ:V → V with ϕ(W) = W and ϕ(v) ≡ v (mod W) for every v ∈ V. We show that GL(3, 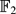) • 1k-3 is, in some sense, the smallest subgroup of GL(V)≅ GL(k, 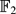, whose invariants are hit by the Steenrod algebra acting on the polynomial algebra, 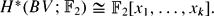. The result is some aspect of an algebraic version of the classical conjecture that the only spherical classes inQ0S0are the elements of Hopf invariant one and those of Kervaire invariant one.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 142 , Issue 1 , January 2007 , pp. 63 - 71
Copyright
Copyright © Cambridge Philosophical Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A.. Atlas of Finite Groups. Maximal Subgroups and Ordinary Characters for Simple Groups. With computational assistance from J. G. Thackray. (Oxford University Press, 1985), xxxiv + 252 pp.Google Scholar
[2] NguyỄn H. V. HƯng. Spherical classes and the algebraic transfer. Trans. Amer. Math. Soc. 349 (1997), 3893–3910.CrossRefGoogle Scholar
[3] NguyỄn H. V. HƯng and Tr n Ng c Nam. The hit problem for the Dickson algebra. Trans. Amer. Math. Soc. 353 (2001), 5029–5040.CrossRefGoogle Scholar
[4] NguyỄn H. V. HƯng and Tr n Ng c Nam. The hit problem for the modular invariants of linear groups. Jour. Algebra 246 (2001), 367–384.CrossRefGoogle Scholar
[5] Kameko, M.. Products of Projective Spaces as Steenrod Modules. Thesis (Johns Hopkins University, 1990).Google Scholar
[6] Peterson, F. P.. Generators of as a module over the Steenrod algebra. Abstracts Amer. Math. Soc., No 833 (1987).Google Scholar
[7] Priddy, S.. On characterizing summands in the classifying space of a group, I. Amer. Jour. Math. 112 (1990), 737–748.CrossRefGoogle Scholar
[8] Singer, W. M.. The transfer in homological algebra. Math. Zeit. 202 (1989), 493–523.CrossRefGoogle Scholar
[9] Suzuki, M.. Group Theory (Springer-Verlag, 1982).Google Scholar
[10] Wood, R. M. W.. Modular representations of and homotopy theory. Lecture Notes in Math. 1172 (Springer-Verlag, 1985), 188–203.Google Scholar