Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-20T16:18:36.464Z Has data issue: false hasContentIssue false
  • English
  • Français

A simple random walk and an associated asymptotic behaviour of the Bessel functions

Published online by Cambridge University Press:  24 October 2008

J. Keilson
J. Keilson
Affiliation:
Applied Research LaboratorySylvania Electronic Systems100 First Avenue, Waltham 54, Mass., U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

We consider a random walk defined in the following way. We have a set of states indexed by n where n takes on all negative and positive integral values and zero. When we are at state n, there is a probability per unit time λ of going to n + 1, and a probability per unit time λ of going to n − l. Let us start out at n = 0, and study Wn(t), the probability of being at n at time t. 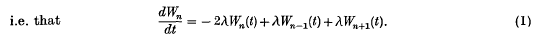Continuity of probability requires that 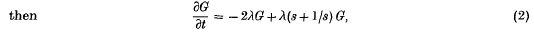whence since G(s, 0) = 1, we have 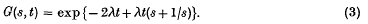It follows from the well-known result .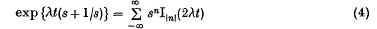

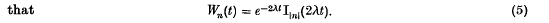Type
Research Notes
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 58 , Issue 4 , October 1962 , pp. 708 - 709
Copyright
Copyright © Cambridge Philosophical Society 1962

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)