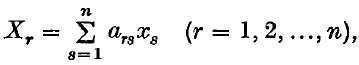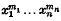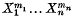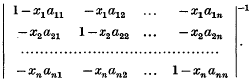Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Good, I. J.
1962.
Proofs of some ‘binomial’ identities by means of MacMahon's ‘Master Theorem’.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 58,
Issue. 1,
p.
161.
Good, I. J.
1965.
The generalization of Lagrange's expansion and the enumeration of trees.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 2,
p.
499.
Carlitz, L.
1974.
An Application of MacMahon’s Master Theorem.
SIAM Journal on Applied Mathematics,
Vol. 26,
Issue. 2,
p.
431.
Egorychev, G. P.
and
Yuzhakov, A. P.
1975.
The determination of generating functions and combinatorial sums by multidimensional residues.
Siberian Mathematical Journal,
Vol. 15,
Issue. 5,
p.
740.
Carlitz, L.
1977.
Some Expansions and Convolution Formulas Related to MacMahon’s Master Theorem.
SIAM Journal on Mathematical Analysis,
Vol. 8,
Issue. 2,
p.
320.
Jackson, D. M.
and
Goulden, I. P.
1979.
A Formal Calculus for the Enumerative System of Sequences—I. Combinatorial Theorems.
Studies in Applied Mathematics,
Vol. 61,
Issue. 2,
p.
141.
Jackson, D. M.
and
Goulden, l. P.
1979.
A Formal Calculus for the Enumerative System of Sequences—II. Applications.
Studies in Applied Mathematics,
Vol. 61,
Issue. 3,
p.
245.
Jackson, D. M.
and
Goulden, I. P.
1980.
A Formal Calculus for the Enumerative System of Sequences—III. Further Developments.
Studies in Applied Mathematics,
Vol. 62,
Issue. 2,
p.
113.
Huang, I-Chiau
1997.
Applications of residues to combinatorial identities.
Proceedings of the American Mathematical Society,
Vol. 125,
Issue. 4,
p.
1011.
Huang, I-Chiau
1998.
Reversion of power series by residues.
Communications in Algebra,
Vol. 26,
Issue. 3,
p.
803.
Konvalinka, Matjaž
and
Pak, Igor
2007.
Non-commutative extensions of the MacMahon Master Theorem.
Advances in Mathematics,
Vol. 216,
Issue. 1,
p.
29.
Foata, Dominique
and
Han, Guo-Niu
2007.
A new proof of the Garoufalidis–Lê–Zeilberger quantum MacMahon Master Theorem.
Journal of Algebra,
Vol. 307,
Issue. 1,
p.
424.
Huang, I-Chiau
2009.
Advances in Combinatorial Mathematics.
p.
127.
Chabaud, Ulysse
Deshpande, Abhinav
and
Mehraban, Saeed
2022.
Quantum-inspired permanent identities.
Quantum,
Vol. 6,
Issue. ,
p.
877.
Chu, Wenchang
2022.
Multiple Derivative Inversions and Lagrange-Good Expansion Formulae.
Mathematics,
Vol. 10,
Issue. 22,
p.
4234.
Kocharovsky, Vitaly V.
Kocharovsky, Vladimir V.
and
Tarasov, Sergey V.
2022.
The Hafnian Master Theorem.
Linear Algebra and its Applications,
Vol. 651,
Issue. ,
p.
144.
Issa, Hassan
Abbas, Hassane
and
Mourad, Bassam
2023.
On an integral representation of the normalized trace of thek-th symmetric tensor power of matrices and some applications.
Linear and Multilinear Algebra,
Vol. 71,
Issue. 7,
p.
1198.