No CrossRef data available.
A semigroup embedding problem and an arithmetical function
Published online by Cambridge University Press: 24 October 2008
Extract
For unexplained terms in semigroup theory see [1] or [4].
Let C, D be classes of semigroups such that every finite semigroup in the class C is embeddable in a finite semigroup in the class D. If n ≥ 2 then k is said to be a C – Dcover of n if every semigroup of order n in the class C is embeddable in a semigroup in the class D of order not greater than k. Let 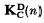 be the least C – D cover of n.
be the least C – D cover of n.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 2 , March 1991 , pp. 277 - 286
- Copyright
- Copyright © Cambridge Philosophical Society 1991
References
REFERENCES
[1]Clifford, A. H. and Preston, G. B.. The algebraic theory of semigroups, vol. 1. Math. Surveys no. 7 (American Mathematical Society, 1961).Google Scholar
[2]Giraldes, E.. Semigroups of high rank. II. Doubly noble semigroups. Proc. Edinburgh Math. Soc. (2) 28 (1985), 409–417.CrossRefGoogle Scholar
[3]Giraldes, E. and Howie, John M.. Semigroups of high rank. Proc. Edinburgh Math. Soc. (2) 28 (1985), 13–34.CrossRefGoogle Scholar
[5]Howie, John M.. Idempotents in completely 0-simple semigroups. Glasgow Math. J. 19 (1978), 109–113.CrossRefGoogle Scholar
[6]Howie, John M.. Embedding semigroups in semibands; some arithmetical results. Quart. J. Math. Oxford Ser. (2) 32 (1981), 323–337.CrossRefGoogle Scholar
[7]Howie, John M.. Arithmetical aspects of semigroup embeddings. In Proceedings Lisbon Conference on Lattices, Semigroups and Universal Algebra. (To appear.)Google Scholar


