Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T07:53:49.888Z Has data issue: false hasContentIssue false
  • English
  • Français

The scroll of tangents of an elliptic quartic curve

Published online by Cambridge University Press:  24 October 2008

W. L. Edge
W. L. Edge
Affiliation:
Inveresk House, Musselburgh EH21 7UA
Get access Rights & Permissions [Opens in a new window]

Extract

1. The equation 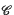of the scroll R of tangents of the curve Γ of intersection of two quadrics in general position in [3] was found by Cayley in 1850 ((l), p. 50). Cayley also considered special positions of the quadrics but we shall not be concerned with these. 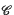was reproduced in Salmon's treatise ((8), p. 191) and Salmon, on this same page, provides an equation in covariant form and so applicable to pairs of quadrics whether in canonical form, or in general position, or not.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 1 , July 1979 , pp. 1 - 11
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cayley, A.On the developable surfaces which arise from two surfaces of the second order. Cambridge and Dublin Math. J. 5 (1850), 46–57; Collected Math. Papers, I, 486–495.Google Scholar
(2)Cayley, A.A memoir on the theory of reciprocal surfaces. Phil. Trans. Royal Soc. 159 (1869), 201–229; Collected Math. Papers vi, 329–358.Google Scholar
(3)Cayley, A.A memoir on quartic surfaces. Proc. London Math. Soc. (1) 3 (1869–1871), 19–69; Collected Math. Papers VII, 133–181.CrossRefGoogle Scholar
(4)Dye, R. H.Pencils of elliptic quartics and an identification of Todd's quartic combinant. Proc. London Math. Soc. (3) 34 (1977), 459–478.CrossRefGoogle Scholar
(5)Edge, W. L.The net of quadric surfaces associated with a pair of Möbius tetrads. Proc. London Math. Soc. (2) 41 (1936), 337–360.CrossRefGoogle Scholar
(6)Enriques, F.Teoria geometrica delle equazioni, in (Bologna, Zanichelli, 1924).Google Scholar
(7)Grace, J. H. and Young, A.Algebra of invariants (Cambridge University Press, 1903).Google Scholar
(8)Salmon, G.A treatise on the analytical geometry of three dimensions, 4th ed. (Dublin, 1882).Google Scholar
(9)Todd, J. A.Combinants of a pencil of quadric surfaces. Proc. Cambridge Phil. Soc. 43 (1947), 475–487.CrossRefGoogle Scholar
(10)Todd, J. A.On the quartic combinant of a pencil of quadric surfaces. Annali di mat. (4) 28 (1949), 189–193.CrossRefGoogle Scholar
(11)Zeuthen, H. G.Revision et extension des formules numériques de la théorie des surfaces réciproques. Math. Annalen 10 (1876), 446–546.CrossRefGoogle Scholar
(12)Zindler, K.Algebraische Liniengeometrie. In Encyklopädie der Math. Wissenschaften, III, C 8.Google Scholar