Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Osgood, Brad
1998.
Quasiconformal Mappings and Analysis.
p.
275.
Chuaqui, M.
and
Pommerenke, Ch.
1999.
Characteristic properties of Nehari functions.
Pacific Journal of Mathematics,
Vol. 188,
Issue. 1,
p.
83.
Chuaqui, M.
Duren, P.
and
Osgood, B.
2007.
Univalence criteria for lifts of harmonic mappings to minimal surfaces.
Journal of Geometric Analysis,
Vol. 17,
Issue. 1,
p.
49.
Hernández Reyes, Rodrigo
2007.
Schwarzian derivatives and some criteria for univalence in.
Complex Variables and Elliptic Equations,
Vol. 52,
Issue. 5,
p.
397.
Chuaqui, Martin
Duren, Peter
and
Osgood, Brad
2009.
Two-point distortion theorems for harmonic mappings.
Illinois Journal of Mathematics,
Vol. 53,
Issue. 4,
Ponnusamy, S.
Qiao, J.
and
Wang, X.
2010.
Schwarzian derivative, integral means, and the affine and linear invariant families of biharmonic mappings.
Applied Mathematics and Computation,
Vol. 216,
Issue. 12,
p.
3468.
Chuaqui, Martin
Duren, Peter
Ma, William
Mejía, Diego
Minda, David
and
Osgood, Brad
2011.
Schwarzian norms and two-point distortion.
Pacific Journal of Mathematics,
Vol. 254,
Issue. 1,
p.
101.
Ma, W.
Mejia, D.
and
Minda, D.
2013.
Bounded Schwarzian and Two-Point Distortion.
Computational Methods and Function Theory,
Vol. 13,
Issue. 4,
p.
705.
Chuaqui, Martin
and
Hernández, Rodrigo
2024.
Families of homomorphic mappings in the polydisk.
Complex Variables and Elliptic Equations,
Vol. 69,
Issue. 9,
p.
1537.


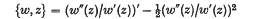
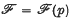 denote the class of functions
denote the class of functions