No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
A Cremona transformation Tn, n′ between two three-dimensional spaces is said to be monoidal if the surfaces of order n in one space which form the homaloidal system corresponding to the planes of the second space have a fixed (n − 1)-ple point O. If the surfaces of order n′ forming the homaloidal system in the second space have a fixed (n′ − 1)-ple point O′, the transformation is said to be bimonoidal. A particularly simple bimonoidal transformation is that which transforms lines through O into lines through O′, and planes through O into planes through O′. Such a transformation we shall call an M-transformation. Its equations can, by suitable choice of coordinates, be expressed in the form
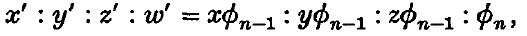
where φn−1(x, y, z, w) = 0, φn(x, y, z, w) = 0 are monoids with vertex (0, 0, 0, 1).
* Pascal, E., Repertorium der höheren Mathematik, ii 2 (Leipzig, 1922), 1032.Google Scholar
† Hudson, H. P., Cremona Transformations (Cambridge, 1927), p. 172.Google Scholar
‡ This transformation is used for the same purpose by Sharpe, F. R. and Snyder, V., “Certain types of involutorial space transformation”, Trans. American Math. Soc. 20 (1919), 185–202CrossRefGoogle Scholar (201).
* Hudson H. P., loc. cit., pp. 306 et seq.
† Montesano, D., “Su le trasformazioni involutorie monoidali”, Rend. Ist. Lombardo (2), 21 (1888), 579–94, 684–7.Google Scholar
‡ Snyder, V., “On the types of monoidal involutions”, Annals of Math. (2), 25 (1924), 279–84.CrossRefGoogle Scholar See also the paper by Sharpe and Snyder previously quoted.