Representation of tiled matrix rings as full matrix rings
Published online by Cambridge University Press: 24 October 2008
Extract
It can be very difficult to determine whether or not certain rings are really full matrix rings. For example, let p be an odd prime, let H be the ring of quaternions over the integers localized at p, and set
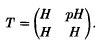
Then T is not presented as a full matrix ring, but there is a subring W of H such that T ≅ M2(W). On the other hand, if we take H to be the ring of quaternions over the integers and form T as above, then it is not known whether T ≅ M2(W) for some ring W. The significance of p being an odd prime is that H/pH is a full 2 x 2 matrix ring, whereas H/2H is commutative. Whether or not a tiled matrix ring such as T above can be re-written as a full matrix ring depends on the sizes of the matrices involved in T and H/pH. To be precise, let H be a local integral domain with unique maximal ideal M and suppose that every one-sided ideal of H is principal. Then H/M ≅ Mk(D) for some positive integer k and division ring D. Given a positive integer n. let T be the tiled matrix ring consisting of all n x n matrices with elements of H on and below the diagonal and elements of M above the diagonal. We shall show in Theorem 2.5 that there is a ring W such that T ≅ Mn(W) if and only if n divides k. An important step in the proof is to show that certain idempotents in T/J(T) can be lifted to idempotents in T, where J(T) is the Jacobson radical of T. This technique for lifting idempotents also makes it possible to show that there are (k + n − 1)!/ k!(n−1)! isomorphism types of finitely generated indecomposable projective right T-modules (Theorem 2·10).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 67 - 72
- Copyright
- Copyright © Cambridge Philosophical Society 1989
References
REFERENCES
- 7
- Cited by


