Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-29T18:56:50.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Representation of Radon shape diffusions via hyperspherical Brownian motion

Published online by Cambridge University Press:  01 September 2008

VICTOR M. PANARETOS
VICTOR M. PANARETOS*
Affiliation:
Department of Statistics, University of California, Berkeley, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A framework is introduced for the study of general Radon shape diffusions, that is, shape diffusions induced by projections of randomly rotating shapes. This is done via a convenient representation of unoriented Radon shape diffusions in (unoriented) D.G. Kendall shape space 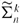through a Brownian motion on the hypersphere. This representation leads to a coordinate system for the generalized version of Radon diffusions since it is shown that shape can be essentially identified with unoriented shape in the projected case. A bijective correspondence between Brownian motion on real projective space and Radon shape diffusions is established. Furthermore, equations are derived for the general (unoriented) Radon diffusion of shape-and-size, and stationary measures are discussed.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 2 , September 2008 , pp. 457 - 470
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carne, T. K.. The geometry of shape spaces. Proc. London Math. Soc. 61 (1990), 407–432.CrossRefGoogle Scholar
[2]Glaeser, R. M.. Review: electron crystallography: present excitement, a nod to the past, anticipating the future. J. Struct. Biol. 128 (1999), 3–14.CrossRefGoogle Scholar
[3]Glaeser, R. M., Chiu, W., Frank, J., DeRosier, D., Baumeister, W. and Downing, K.. Electron Crystallography of Biological Macromolecules (Oxford University Press, 2007).CrossRefGoogle Scholar
[4]Dryden, I. L. and Mardia, K. V.. Statistical Shape Analysis (Wiley, 1998).Google Scholar
[5]James, A. T.. Distributions of matrix variates and latent roots derived from normal samples. Ann. Math. Stat. 35 (1964), (2), 475–501.CrossRefGoogle Scholar
[6]Kendall, D. G.. The diffusion of Euclidean shape. Adv. App. Prob. 9 (1977), 428–430.Google Scholar
[7]Kendall, D. G., Barden, D., Carne, T. K. and Le, H.. Shape and Shape Theory (Wiley, 1999).CrossRefGoogle Scholar
[8]Kendall, W. S.. Stochastic differential geometry: an introduction. Acta Appl. Math. 9 (1987), 29–60.CrossRefGoogle Scholar
[9]Kendall, W. S.. The Euclidean diffusion of shape. In Disorder in Physical Systems, ed. Grimmett, G. and Welsh, D. (Cambridge University Press, 1990), 203–217.Google Scholar
[10]Kendall, W. S.. A diffusion model for Bookstein triangle shape. Adv. App. Prob. 30 (1998), 317–334.CrossRefGoogle Scholar
[11]Le, H.. On geodesics in Euclidean shape spaces. J. London Math. Soc. (2), 44 (1990), 360–372.Google Scholar
[12]Le, H. and Kendall, D. G.. The Riemannian structure of Euclidean shape spaces: a novel environment for statistics. Ann. Stat. 21 (1993), (3), 1225–1271.CrossRefGoogle Scholar
[13]Mardia, K. V. and Khatri, C.G.. Uniform distribution on a Stiefel manifold. J. Multivariate Anal. 7 (1975), 468–473.CrossRefGoogle Scholar
[14]Mosteller, F. and Tukey, J. W.. Data Analysis and Regression: a Second Course in Statistics (Addison-Wesley, 1977).Google Scholar
[15]Øksendal, B.. Stochastic Differential Equations (Springer, 2003).CrossRefGoogle Scholar
[16]Panaretos, V. M.. The diffusion of Radon shape. Adv. App. Prob. 38 (2) (2006), 320–335.CrossRefGoogle Scholar
[17]Panaretos, V. M.. Representation of Radon shape diffusions via hyperspherical Brownian motion. Tech. Report #707, Department of Statistics, UC Berkeley (April 2006).Google Scholar
[18]Price, G. C. and Williams, D.. Rolling without slipping, I. In Séminaire de Probabilités XVII-1981/82 (Paris), Lecture Notes in Mathematics 986 (Springer-Verlag, 1983)Google Scholar
[19]Rogers, L. C. G. and Williams, D.. Diffusions, Markov Processes and Martingales. Volume 2: Itô calculus. Cambridge Mathematical Library (Cambridge University Press, 2000).Google Scholar
[20]Small, C. G.. The Statistical Theory of Shape (Springer, 1996).CrossRefGoogle Scholar
[21]Stoyan, D., Kendall, W. S. and Mecke, J.. Stochastic Geometry and its Applications (Wiley, 1995).Google Scholar
[22]Van Den Berg, M. and Lewis, J. T.. Brownian motion on a hypersurface. Bull. London Math. Soc. 17 (1985), 144–150.CrossRefGoogle Scholar
[23]Watson, G. S.. Statistics on Spheres (Wiley, 1983).Google Scholar