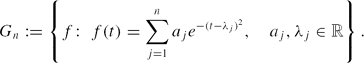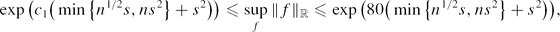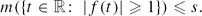Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pierzchała, Rafał
2015.
Remez-type inequality on sets with cusps.
Advances in Mathematics,
Vol. 281,
Issue. ,
p.
508.
Erdélyi, Tamás
2017.
Progress in Approximation Theory and Applicable Complex Analysis.
Vol. 117,
Issue. ,
p.
19.
Erdélyi, Tamás
2019.
Topics in Classical and Modern Analysis.
p.
135.


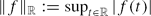 and
and