Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T19:37:20.584Z Has data issue: false hasContentIssue false
  • English
  • Français

Reflections in extended Bianchi groups

Published online by Cambridge University Press:  24 October 2008

L. Ya. Vulakh
L. Ya. Vulakh
Affiliation:
Department of Mathematics, The Cooper Union, 51 Astor Place, New York, NY 10003, USA
Get access Rights & Permissions [Opens in a new window]

Extract

Let d be a positive square-free number. Let Od be the ring of integers in Q(√ −d). The groups PSL(2, Od) are called collectively the Bianchi groups. The extended Bianchi group Bd is the maximal discrete extension of PSL(2, Od) in PSL(2, C). The group Bd acts by linear fractional transformations on the complex plane C. Let RBd be Bd with the generator θ, 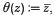, adjoined. (RBd will be also called an extended Bianchi group (cf. [18])). A group is said to be reflective if it contains a Coxeter subgroup (i.e. a subgroup generated by reflections) of finite index. The groups RBd and their subgroups have been investigated in [3, 6, 13, 15, 16, 17, 18, 20, 21]. In 1892 Bianchi[3] proved that PGL(2, Od)⋊{θ} is reflective if d ≤ 19, d ╪ 14 or 17. Vinberg [18] proved that if the group RBd is reflective, then the orders of all elements of the ideal-class group of the field Q(√ −d) should divide 4. Shaiheev [16] proved that there are only finitely many reflective extended Bianchi groups and found all of them for d ≤ 30. Similar results are obtained for groups PGL(2, Od) ⋊ {θ} which, as Shvartsman [17] showed, are reflective only when d = 1, 2, 5, 6, 10, 13, 21, provided d = 1 or 2 (mod 4).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 13 - 25
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beardon, A. F.. The Geometry of Discrete Groups (Springer-Verlag, 1983).CrossRefGoogle Scholar
[2]Baskan, T. and Macbeath, A. M.. Centralizers of reflections in crystallographic groups. Math. Proc. Cambridge Phil. Soc. 79 (1982), 79–91.CrossRefGoogle Scholar
[3]Bianchi, L.. Sui gruppi di sostituzioni lineari con coefficienti appartenenti a corpi quadratici immaginari. Math. Ann. 40 (1892), 332–412.CrossRefGoogle Scholar
[4]Borevich, Z. I. and Shafarevich, I. R.. Number Theory (Academic Press, 1966).Google Scholar
[5]Cassels, J. W. S.. Rational Quadratic Forms (Academic Press, 1978).Google Scholar
[6]Elstrodt, J., Grunewald, F. and Mennicke, J.. Discontinuous groups on three-dimensional hyperbolic space: analytic theory and arithmetic applications. Russian Math. Surveys 38 (1) (1983) 137–168.CrossRefGoogle Scholar
[7]Elstrodt, J., Grunewald, F. and Mennicke, J.. Zeta-functions of binary Hermitian forms and special values of Eisenstein series. Math. Ann. 277 (1987), 655–708.CrossRefGoogle Scholar
[8]Ford, L. R.. Automorphic Functions, 2nd ed. (Chelsea, New York, 1951).Google Scholar
[9]Jones, B. W.. The Arithmetic Theory of Quadratic Forms, Carus Math. Monograph No. 10. (Math. Assoc. Amer., Washington, D.C., 1950).CrossRefGoogle Scholar
[10]Maclachlan, C.. Fuchsian subgroups of the groups PSL2(Od). In Durham Conference on Hyperbolic Geometry. London Math. Soc. Lecture Notes Series, 112 (Cambridge Univ. Press 1986), 303–311.Google Scholar
[11]Maclachlan, C. and Reid, A. W.. Commensurability classes of arithmetic Kleinian groups and their Fuchsian subgroups. Math. Proc. Cambridge Phil. Soc. 102 (1987), 251–257.CrossRefGoogle Scholar
[12]Margulis, G. A.. Discrete Subgroups and Ergodic Theory. In Number Theory, Trace Formula and Discrete Groups. Symposium in honor of Atle Selberg held at the University of Oslo, Oslo, 06 14–20, 1987. Edited by Egil Aubert, Karl, Bombieri, Enrrico and Goldfeld, Dorian. (Academic Press, 1989).Google Scholar
[13]Ruzmanov, O. P.. Reflection subgroups of Bianchi groups. Uspekhi Mat. Nauk 45 (1990), no. 1 (2711), 189–190; (translated inGoogle Scholar
Russian Math. Surveys 45 (1990), no. 1, 227–228.Google Scholar
[14]Serre, J. P.. A course in Arithmetic (Springer, 1973).CrossRefGoogle Scholar
[15]Swan, R. G.. Generators and relations for certain special linear groups. Adv. in Math. 6 (1971), 1–77.CrossRefGoogle Scholar
[16]Shaiheev, M. K.. Reflective Subgroups in Bianchi Groups. In Problems in Group Theory and Homological Algebra. Yaroslavl State University, 1987, pp. 127–133, translated inGoogle Scholar
Sel. Math. Sov, 9:4 (1990), 315–322.Google Scholar
[17]Shvartsman, O. V.. Reflective Subgroups of Bianchi Groups. In Problems in Group Theory and Homological Algebra (Yaroslavl State University, 1987), translated inGoogle Scholar
Sel. Math. Sov, 9:4 (1990), 323–329.Google Scholar
[18]Vinberg, E. B.. Reflective Subgroups in Bianchi Groups. In Problems in Group Theory and Homological Algebra (Yaroslavl State University, 1987), pp. 121–127, translated inGoogle Scholar
Sel. Math. Sov, 9:4 (1990), 309–314.Google Scholar
[19]Vulakh, L. Ya.. On minima of rational indefinite Hermitian forms. Ann. N.Y. Acad. Sci. 410 (1983), 99–106.CrossRefGoogle Scholar
[20]Vulakh, L. Ya.. Classification of Fuchsian subgroups of some Bianchi groups. Canad. Math. Bull. 34 (3), (1991) 417–422.CrossRefGoogle Scholar
[21]Vulakh, L. Ya.. Maximal Fuchsian subgroups of extended Bianchi groups. In Number Theory with Emphasis on the Markoff Spectrum, eds. Pollington, A. and Moran, W. (Marcel Dekker, Inc., New York, 1993).Google Scholar