In this article we investigate the meromorphic differential equation X′(z) = A(z) X(z), often abbreviated by [A], where A(z) is a matrix (all matrices we consider have dimensions 2 × 2) meromorphic at infinity, i.e. holomorphic in a punctured neighbourhood of infinity with at most a pole there. Moreover, X(z) denotes a fundamental solution matrix. Given a matrix T(z) which together with its inverse is meromorphic at infinity (a meromorphic transformation), then the function Y(z) = T−1(z) X(z) solves the differential equation [B] with B = T−1AT − T−1T [1,5]. This introduces an equivalence relation among meromorphic differential equations and leads to the question of finding a simple representative for each equivalence class, which, for example, is of importance for further function-theoretic examinations of the solutions. The first major achievement in this direction is marked by Birkhoff's reduction which shows that it is always possible to obtain an equivalent equation [B] where B(z) is holomorphic in ℂ ¬ {0} (throughout this article A ¬ B denotes the difference of these sets) with at most a singularity of the first kind at 0 [1, 2, 5, 6]. We call this the standard form. The question of how many further simplifications can be made will be answered in the framework of our reduction theory. For this purpose we introduce the notion of a normalized standard equation [A] (NSE) which is defined by the following conditions:

(i) 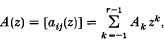, where r ∈ ℕ and Ak are constant matrices, (notation: )

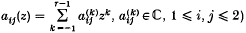(ii) A(z) has trace tr 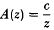for some c ∈ ℂ,

(iii) Ar−1 has different eigenvalues,

(iv) the eigenvalues of A−1 are either incongruent modulo 1 or equal,

(v) if A−1 = μI, then Ar−1 is diagonal,

(vi) Ar−1 and A−1 are triangular in opposite ways,

(vii) a12(z) is monic (leading coefficient equals 1) unless a12 ≡ 0; furthermore a21(z) is monic in case that a12 ≡ 0 but a21 ≢ 0.