Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T17:08:00.216Z Has data issue: false hasContentIssue false
  • English
  • Français

A rational invariant for certain infinite discrete groups

Published online by Cambridge University Press:  24 October 2008

F. E. A. Johnson
F. E. A. Johnson
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT
Get access Rights & Permissions [Opens in a new window]

Extract

We introduce a rational-valued invariant which is capable of distinguishing between the commensurability classes of certain discrete groups, namely, the fundamental groups of smooth closed orientable aspherical manifolds of dimensional 4k(k ≥ 1) whose Euler characteristic χ(Λ) is non-zero. The invariant in question is the quotient

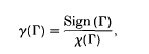
where Sign (Λ) is the absolute value of the signature of the intersection form

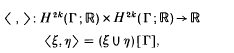
and [Λ] is a generator of H4k(Λ; ℝ).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 3 , May 1993 , pp. 473 - 478
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Atiyah, M. F.. The signature of fibre bundles. In Collected Papers in Honour of K. Kodaira (Tokyo University Press, 1969), pp. 73–84.Google Scholar
[2]Hirzebruch, F.. The signature of ramified coverings. In Collected Papers in Honour of K. Kodaira (Tokyo University Press, 1969), pp. 253–265.Google Scholar
[3]Kodaira, K.. A certain type of irregular algebraic surface. J. Analyse Math. 19 (1967), 207–215.CrossRefGoogle Scholar
[4]Mostow, G. B. and Siu, Y. T.. A compact Kähler surface of negative curvature not covered by the ball. Ann. of Math. 112 (1980), 321–360.CrossRefGoogle Scholar