Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T07:50:00.288Z Has data issue: false hasContentIssue false
  • English
  • Français

The rank of the semigroup of transformations stabilising a partition of a finite set

Published online by Cambridge University Press:  06 July 2015

JOÃO ARAÚJO ,
WOLFRAM BENTZ ,
JAMES D. MITCHELL  and
CSABA SCHNEIDER
JOÃO ARAÚJO
Affiliation:
Universidade Aberta, R. Escola Politécnica, 147, 1269-001 Lisboa, Portugal & CEMAT-CIÊNCIAS, Departamento de Matemática, Faculdade de Ciências, Universidade de Lisboa, 1749-016, Lisboa, Portugal. e-mail: [email protected]
WOLFRAM BENTZ
Affiliation:
CEMAT-CIÊNCIAS, Departamento de Matemática, Faculdade de Ciências, Universidade de Lisboa, 1749-016, Lisboa, Portugal. e-mail: [email protected]
JAMES D. MITCHELL
Affiliation:
School of Mathematics and Statistics, University of St Andrews, North Haugh, St Andrews, Fife, KY16 9SS, Scotland. e-mail: [email protected]
CSABA SCHNEIDER
Affiliation:
Departamento de Matemática, Instituto de Ciências Exatas, Universidade Federal de Minas Gerais, Av. Antônio Carlos, 6627, Caixa Postal 702, 31270-901 Belo Horizonte, MG, Brazil. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

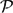Let $\mathcal{P}$ be a partition of a finite set X. We say that a transformation f : X → X preserves (or stabilises) the partition 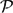$\mathcal{P}$ if for all P ∈ 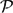$\mathcal{P}$ there exists Q ∈ 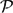$\mathcal{P}$ such that Pf ⊆ Q. Let T(X, 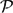$\mathcal{P}$) denote the semigroup of all full transformations of X that preserve the partition 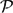$\mathcal{P}$.

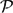In 2005 Pei Huisheng found an upper bound for the minimum size of the generating sets of T(X, $\mathcal{P}$), when 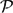$\mathcal{P}$ is a partition in which all of its parts have the same size. In addition, Pei Huisheng conjectured that his bound was exact. In 2009 the first and last authors used representation theory to solve Pei Huisheng's conjecture.

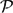The aim of this paper is to solve the more complex problem of finding the minimum size of the generating sets of T(X, $\mathcal{P}$), when 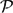$\mathcal{P}$ is an arbitrary partition. Again we use representation theory to find the minimum number of elements needed to generate the wreath product of finitely many symmetric groups, and then use this result to solve the problem.

The paper ends with a number of problems for experts in group and semigroup theories.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 2 , September 2015 , pp. 339 - 353
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] André, J., Araújo, J. and Konieczny, J. Regular centralizers of idempotent transformations. Semigroup Forum. 82 (2011), 307–318.Google Scholar
[2] Araújo, J. and Konieczny, J. A method for finding new sets of axioms for classes of semigroups. Archives for Mathematical Logic. 51 (2012), 461–474.Google Scholar
[3] Araújo, J. and Konieczny, J. Semigroups of transformations preserving an equivalence relation and a cross-section. Comm. in Algebra. 32 (2004), 1917–1935.Google Scholar
[4] Araújo, J. and Konieczny, J. Automorphisms groups of centralizers of idempotents. J. Algebra. 269 (2003), 227–239.Google Scholar
[5] Araújo, J. and Mitchell, J. D. Relative ranks in the monoid of endomorphisms of an independence algebra. Monatsh. Math. 151 (1) (2007), 1–10.Google Scholar
[6] Araújo, J., Mitchell, J. D., and Silva, N. On generating countable sets of endomorphisms. Algebra Universalis. 50 (1) (2003), 61–67.Google Scholar
[7] Araújo, J. and Schneider, C. The rank of the endomorphism monoid of a uniform partition. Semigroup Forum. 78 3 (2009), 498–510.Google Scholar
[8] Banach, S. Sur un theorème de M. Sierpiński. Fund. Math. 25 (1935), 5–6.Google Scholar
[9] Barnes, G. and Levi, I. Ranks of semigroups generated by order-preserving transformations with a fixed partition type. Comm. Algebra. 31 (4) (2003), 1753–1763.Google Scholar
[10] Barnes, G. and Levi, I. On idempotent ranks of semigroups of partial transformations. Semigroup Forum. 70 (1) (2005), 81–96.Google Scholar
[11] Cichoń, J., Mitchell, J. D. and Morayne, M. Generating continuous mappings with Lipschitz mappings. Trans. Amer. Math. Soc. 359 (5) (2007), 2059–2074 (electronic).Google Scholar
[12] Garba, G. U. On the nilpotent ranks of certain semigroups of transformations. Glasgow Math. J. 36 (1) (1994), 1–9.Google Scholar
[13] Gomes, G. M. S. and Howie, J. M. On the ranks of certain semigroups of order-preserving transformations. Semigroup Forum. 45 (3) (1992), 272–282.Google Scholar
[14] Higgins, P. M., Howie, J. M., Mitchell, J. D., and Ruškuc, N. Countable versus uncountable ranks in infinite semigroups of transformations and relations. Proc. Edinburgh Math. Soc. (2). 46 (3) (2003), 531–544.Google Scholar
[15] Higgins, P. M., Mitchell, J. D., Morayne, M. and Ruškuc, N. Rank properties of endomorphisms of infinite partially ordered sets. Bull. London Math. Soc. 38 (2) (2006), 177–191.Google Scholar
[16] Higgins, P. M., Howie, J. M., and Ruškuc, N. Generators and factorisations of transformation semigroups. Proc. Roy. Soc. Edinburgh Sect. A. 128 (6) (1998), 1355–1369.Google Scholar
[17] Howie, J. M. Fundamentals of semigroup theory vol. 12, London Math. Soc. Monogr. New Series. (The Clarendon Press, Oxford University Press, New York, 1995, Oxford Science Publications).Google Scholar
[18] Howie, J. M. and McFadden, R. B. Idempotent rank in finite full transformation semigroups. Proc. Roy. Soc. Edinburgh Sect. A. 114 (3–4) (1990), 161–167.Google Scholar
[19] Howie, J. M., Ruškuc, N. and Higgins, P. M. On relative ranks of full transformation semigroups. Comm. Algebra. 26 (3) (1998), 733–748.Google Scholar
[20] Huisheng, P. On the rank of the semigroup TE(X) . Semigroup Forum. 70 (1) (2005), 107–117.Google Scholar
[21] Kleidman, P. and Liebeck, M. The subgroup structure of the finite classical groups. London Math. Soc. Lecture Note Series. vol. 129 (Cambridge University Press, Cambridge, 1990).Google Scholar
[22] Levi, I. Nilpotent ranks of semigroups of partial transformations. Semigroup Forum. 72 (3) (2006), 459–476.Google Scholar
[23] Levi, I. and Seif, S. Combinatorial techniques for determining rank and idempotent rank of certain finite semigroups. Proc. Edinburgh Math. Soc. (2). 45 (3) (2002), 617–630.Google Scholar
[24] Meldrum, J. D. P. Wreath products of groups and semigroups. Pitman Monographs and Surveys in Pure and Applied Mathematics. vol. 74 (Longman, Harlow, 1995).Google Scholar
[25] Mitchell, J. D. et al. Semigroups - GAP package, Version 2.4.1. May 2015. http://www-groups.mcs.st-andrews.ac.uk/~jamesm/semigroups.php Google Scholar
[26] Ribeiro, M. I. M. Rank properties in finite inverse semigroups. Proc. Edinburgh Math. Soc. (2). 43 (3) (2000), 559–568.Google Scholar
[27] Scott, L. L. Representations in characteristic p . In The Santa Cruz Conference on Finite Groups (Univ. California, Santa Cruz, Calif., 1979). Proc. Symp. Pure Math. vol. 37 (Amer. Math. Soc., Providence, R.I., 1980), pages 319–331.Google Scholar
[28] Sierpiński, W. Sur les suites infinies de fonctions définies dans les ensembles quelconques. Fund. Math. 24 (1935), 209–212.Google Scholar
[29] Straubing, H. The wreath product and its applications. In Formal Properties of Finite Automata and Applications (Ramatuelle, 1988). Lecture Notes in Comput. Sci. vol. 386 (Springer, Berlin, 1989), pages 15–24.Google Scholar