Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-10T20:03:54.300Z Has data issue: false hasContentIssue false
  • English
  • Français

Pure Projective Approximations

Published online by Cambridge University Press:  01 January 2009

IVO HERZOG  and
PHILIPP ROTHMALER
IVO HERZOG
Affiliation:
The Ohio State University at Lima, Lima, OH 45804, U.S.A. e-mail: [email protected]
PHILIPP ROTHMALER
Affiliation:
The City University of New York, University Ave and W 181 St, Bronx, NY 10453, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A notion of good behavior is introduced for a definable subcategory 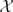of left R-modules. It is proved that every finitely presented left R-module has a pure projective left 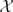-approximation if and only if the associated torsion class 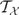of finite type in the functor category (mod-R, Ab) is coherent, i.e., the torsion subobject of every finitely presented object is finitely presented. This yields a bijective correspondence between such well-behaved definable subcategories and preenveloping subcategories of the category Add(R-mod) of pure projective left R-modules. An example is given of a preenveloping subcategory ⊆ Add(R-mod) that does not arise from a covariantly finite subcategory of finitely presented left R-modules. As a general example of this good behavior, it is shown that if R is a ring over which every left cotorsion R-module is pure injective, then the smallest definable subcategory 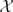(R-proj) containing every finitely generated projective module is well-behaved.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 146 , Issue 1 , January 2009 , pp. 83 - 94
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Angeleri-Hügel, L. and Trlifaj, J.Direct limits of modules of finite projective dimension. In Rings, Modules, Algebras and Abelian Groups, Lecture Notes in Pure and Appl. Math. 236 (Marcel Dekker 2004), 27–44.Google Scholar
[2]Angeleri-Hügel, L., Tonolo, A. and Trlifaj, J.Tilting preenvelopes and cotilting precovers. Algebr. Represent. Theory 4 (2001), 155–170.CrossRefGoogle Scholar
[3]Auslander, M. Coherent functors. In Proceedings of the Conference on Categorical Algebra (La Jolla, CA, 1965), (Springer, 1966), 189–231.CrossRefGoogle Scholar
[4]Auslander, M.A functorial approach to representation theory. In Representations of Algebras (ICRA III, Puebla 1980), Lecture Notes in Math. vol. 944, Springer, 1982, 105–179.CrossRefGoogle Scholar
[5]Auslander, M. Isolated singularities and existence of almost split sequences. Representation Theory II (ICRA IV, Ottawa, 1984), Lecture Notes in Math. vol. 1178 (Springer, 1986), 194–241.Google Scholar
[6]Auslander, M. and Smalø, S.Preprojective modules over artin algebras. J. of Algebra 66 (No 1) (1980), 61–122.CrossRefGoogle Scholar
[7]Crawley-Boevey, W. W. Modules of finite length over their endomorphism rings. In Representations of Algebras and Related Topics, Tachikawa, H. and Brenner, S., eds. London Math. Soc. Lecture Note Series vol. 168 (Cambridge University Press, 1992), 127–184.CrossRefGoogle Scholar
[8]Crawley-Boevey, W. W.Locally finitely presented additive categories. Comm. Algebra 22 (5) (1994), 1641–1674.CrossRefGoogle Scholar
[9]Dubrovin, N. and Puninski, G.Classifying projective modules over some semilocal rings. J. Algebra Appl. 6 (5) (2007), 839–866.CrossRefGoogle Scholar
[10]Enochs, E. E. and Jenda, O. M. G.Relative Homological Algebra. de Gruyter Expositions in Mathematics 30 (Walter de Gruyter, 2000).CrossRefGoogle Scholar
[11]Gruson, L. and Jensen, C. U. Dimensions cohomoligiques reliées aux foncteurs lim(i). In Séminaire d'Algèbre Paul Dubreil et Marie-Paule Malliavin, Paris. Lecture Notes in Math. 867 (Springer-Verlag, 1981), 234–294.CrossRefGoogle Scholar
[12]Herzog, I. and Rothmaler, Ph. When cotorsion modules are pure injective, preprint.Google Scholar
[13]Krause, H.The Spectrum of a Module Category. Mem of Amer. Math. Soc. 149 (707) (2001).Google Scholar
[14]Lenzing, H.Homological transfer from finitely presented to infinite modules. Lecture Notes in Math. vol. 1006 (Springer, 1983), 734–761.CrossRefGoogle Scholar
[15]Prest, M.Model Theory and Modules. London Math. Soc. Lecture Notes Series 130 (Cambridge University Press, 1988).Google Scholar
[16]Puninski, G., Some model theory over a nearly simple uniserial domain and decompositions of serial modules. J. Pure Appl. Algebra 163 (2001), 319–337.CrossRefGoogle Scholar
[17]Rada, J. and Saorin, M.Rings characterized by (pre)envelopes and (pre)covers of their modules. Comm. Algebra 26 (3) (1998), 899–912.CrossRefGoogle Scholar
[18]Raynaud, M. and Gruson, L., Critères de platitude et de projectivité. Invent. Math. 13 (1971), 1–89.CrossRefGoogle Scholar
[19]Stenström, B.Rings of Quotients. (Springer-Verlag, 1996).Google Scholar
[20]Warfield, R. B. Jr.Purity and algebraic compactness for modules. Pacific J. Math. 28 (1969), 699–719.CrossRefGoogle Scholar
[21]Wisbauer, R.Foundations of Module and Ring Theory. (Gordon and Breach, 1991).Google Scholar
[22]Xu, J., Flat Covers of Modules. Lecture Notes in Math. vol. 1634 (Springer, 1996).CrossRefGoogle Scholar