Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-29T23:19:33.474Z Has data issue: false hasContentIssue false
  • English
  • Français

Pure exact structures and the pure derived category of a scheme

Published online by Cambridge University Press:  23 November 2016

SERGIO ESTRADA ,
JAMES GILLESPIE  and
SINEM ODABAŞI
SERGIO ESTRADA
Affiliation:
Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, Espinardo, Murcia 30100, Spain. e-mail: [email protected]
JAMES GILLESPIE
Affiliation:
Ramapo College of New Jersey, School of Theoretical and Applied Science, 505 Ramapo Valley Road, Mahwah, NJ 07430, U.S.A. e-mail: [email protected]
SINEM ODABAŞI
Affiliation:
Instituto de Ciencias Físicas y Matemáticas, Universidad Austral de Chile, Valdivia, Chile. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

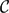Let $\mathcal{C}$ be closed symmetric monoidal Grothendieck category. We define the pure derived category with respect to the monoidal structure via a relative injective model category structure on the category C(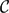$\mathcal{C}$) of unbounded chain complexes in 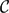$\mathcal{C}$. We use λ-Purity techniques to get this. As application we define the stalkwise pure derived category of the category of quasi–coherent sheaves on a quasi-separated scheme. We also give a different approach by using the category of flat quasi–coherent sheaves.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 163 , Issue 2 , September 2017 , pp. 251 - 264
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AR94] Adamek, J. and Rosicky, J. Locally presentable and accessible categories. London Math. Soc. Lecture Note Series, 189 (Cambridge University Press, Cambridge, 1994).Google Scholar
[Bek00] Beke, T. T. Sheafifiable homotopy model categories. Math. Proc. Camb. Phil. Soc. 129 (3) (2000), 447–475.CrossRefGoogle Scholar
[CH02] Christensen, J. D. and Hovey, M. Quillen model structures for relative homological algebra. Math. Proc. Camb. Phil. Soc. 133 (2) (2002), 261–293.CrossRefGoogle Scholar
[Craw94] Crawley–Boevey, W. Locally finitely presented additive categories. Comm. Algebra 22(1994), 1641–1674.CrossRefGoogle Scholar
[EE016] Enochs, E., Estrada, S. and Odabaşi, S. Pure injective and absolutely pure sheaves. Proc. Edinburgh Math. Soc. 59 (2016), 623–640.CrossRefGoogle Scholar
[ES15] Estrada, S. and Saorín, M. Locally finitely presented categories with no flat objects. Forum Math. 27 (2015), 269–301.CrossRefGoogle Scholar
[Fox76] Fox, T. F. Purity in locally-presentable monoidal categories. J. Pure Appl. Algebra 8 (3) (1976), 261-265.CrossRefGoogle Scholar
[Gil11] Gillespie, J. Model structures on exact categories. J. Pure App. Alg. 215 (2011), 2892–2902.CrossRefGoogle Scholar
[Gil16a] Gillespie, J. Exact model structures and recollements. J. Algebra. 458 (2016), 265–306.CrossRefGoogle Scholar
[Gil16b] Gillespie, J. The derived category with respect to a generator. Ann. Mat. Pura Appl. (4) 195 (2) (2016), 371–402.CrossRefGoogle Scholar
[Hov02] Hovey, M. Cotorsion pairs, model category structures and representation theory. Math. Z. 241 (2002), 553–592.CrossRefGoogle Scholar
[Kra12] Krause, H. Approximations and adjoints in homotopy categories. Math. Ann. 353 (3) (2012), 765–781.CrossRefGoogle Scholar
[MS11] Murfet, D. and Salarian, S. Totally acyclic complexes over noetherian schemes. Adv. Math. 226 (2011), 1096–1133.CrossRefGoogle Scholar
[Pre09] Prest, M. Purity, spectra and localisation. Encyclopedia of Mathematics and its Applications, 121 (Cambridge University Press, Cambridge 2009).Google Scholar
[PR04] Prest, M. and Ralph, A. Locally finitely presented categories of sheaves of modules. Available at: http://www.maths.manchester.ac.uk/~mprest/publications.html.Google Scholar
[Sto13] Šťovíček, J. Exact model categories, approximation theory and cohomology of quasi-coherent sheaves. Advances in representation theory of algebras. EMS Ser. Congr. Rep., Eur. Math. Soc. (Zürich, 2013), pp. 297–367.CrossRefGoogle Scholar