Hostname: page-component-7b9c58cd5d-9klzr Total loading time: 0 Render date: 2025-03-17T04:44:25.866Z Has data issue: false hasContentIssue false
  • English
  • Français

Projections of Poisson cut-outs in the Heisenberg group and the visual 3-sphere

Part of: Global differential geometry Smooth dynamical systems: general theory Classical measure theory Geometric probability and stochastic geometry Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  08 March 2021

LAURENT DUFLOUX  and
VILLE SUOMALA
LAURENT DUFLOUX
Affiliation:
Department of Mathematics and Statistics, P.O. Box 35, FI-40014, University of Jyväskylä, Finland e-mail: [email protected]
VILLE SUOMALA
Affiliation:
Department of Mathematical Sciences, P.O. Box 8000, FI-90014, University of Oulu, Finland e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study projectional properties of Poisson cut-out sets E in non-Euclidean spaces. In the first Heisenbeg group 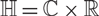\[\mathbb{H} = \mathbb{C} \times \mathbb{R}\], endowed with the Korányi metric, we show that the Hausdorff dimension of the vertical projection 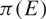\[\pi (E)\] (projection along the center of 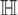\[\mathbb{H}\]) almost surely equals 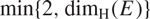\[\min \{ 2,{\dim _\operatorname{H} }(E)\} \] and that 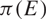\[\pi (E)\] has non-empty interior if 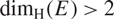\[{\dim _{\text{H}}}(E) > 2\]. As a corollary, this allows us to determine the Hausdorff dimension of E with respect to the Euclidean metric in terms of its Heisenberg Hausdorff dimension \[{\dim _{\text{H}}}(E)\].

We also study projections in the one-point compactification of the Heisenberg group, that is, the 3-sphere 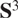\[{{\text{S}}^3}\] endowed with the visual metric d obtained by identifying \[{{\text{S}}^3}\] with the boundary of the complex hyperbolic plane. In \[{{\text{S}}^3}\], we prove a projection result that holds simultaneously for all radial projections (projections along so called “chains”). This shows that the Poisson cut-outs in \[{{\text{S}}^3}\] satisfy a strong version of the Marstrand’s projection theorem, without any exceptional directions.

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 28A80: Fractals 37D35: Thermodynamic formalism, variational principles, equilibrium states 37C45: Dimension theory of dynamical systems 53C17: Sub-Riemannian geometry
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 1 , January 2022 , pp. 197 - 230
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by: Academy of Finland via the Centre of Excellence in Analysis and Dynamics research and the research project Geometry of subRiemannian Groups (#288501), the European Research Council via the ERC Starting Grant #713998 GeoMeG ‘Geometry of Metric Groups’, the Institute Mittag-Leffler via the Fractal Geometry and Dynamics research program.

References

Balogh, Z., Durand–Cartagena, E., Fässler, K., Mattila, P. and Tyson, J. T.. The effect of projections on dimension in the Heisenberg group. Rev. Mat. Iberoam. 29(2) (2013), 381–432.CrossRefGoogle Scholar
Balogh, Z., Rickly, M. and Cassano, F. S.. Comparison of Hausdorff measures with respect to the Euclidean and the Heisenberg metric. Publ. Mat. 47(1) (2003), 237–259.CrossRefGoogle Scholar
Bourbaki, N.. Éléments de mathématique. Algèbre. Chapitre 9, (Springer-Verlag, Berlin, 2007). Reprint of the 1959 original.Google Scholar
Capogna, L., Danielli, D., Pauls, S. D. and Tyson, J. T.. An introduction to the Heisenberg group and the sub-Riemannian isoperimetric problem. Progr. Math. vol. 259 (Birkhäuser Verlag, Basel, 2007).Google Scholar
Dufloux, L.. Hausdorff dimension of limit sets. Geom. Dedicata. 191 (2017), 1–35.CrossRefGoogle Scholar
Dufloux, L.. Linear foliations of complex spheres I. Chains. Preprint. Available online at https://arxiv.org/abs/1703.09553https://arxiv.org/abs/1703.09553 (2017).Google Scholar
Falconer, K. J.. Projections of random Cantor sets. J. Theoret. Probab. 2(1) (1989), 65–70.CrossRefGoogle Scholar
Falconer, K. J. and Grimmett, G. R.. On the geometry of random Cantor sets and fractal percolation. J. Theoret. Probab. 5(3) (1992), 465–485.CrossRefGoogle Scholar
Goldman, W. M.. Complex hyperbolic geometry. Oxford Math. Monogr. (Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1999).Google Scholar
Hochman, M. and Shmerkin, P.. Local entropy averages and projections of fractal measures. Ann. of Math., 12 175(3) (2012), 1001–1059.CrossRefGoogle Scholar
Mandelbrot, B. B.. Renewal sets and random cutouts. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete. 22 (1972), 145–157.CrossRefGoogle Scholar
Mattila, P.. Geometry of sets and measures in Euclidean spaces. Camb. Stud. Adv. Math. vol. 44. (Cambridge University Press, Cambridge, 1995). Fractals and rectifiability.Google Scholar
Ojala, T., Ville, Suomala and Wu, M.. Random cutout sets with spatially inhomogeneous intensities. Israel J. Math. 220(2) (2017), 899–925.CrossRefGoogle Scholar
Quint, J.. An overview of Patterson-Sullivan theory. Lecture notes. Available online at https://www.math.u-bordeaux.fr/jquint/publications/courszurich.pdf (2006).Google Scholar
Rams, M. and Simon, K.. The geometry of fractal percolation. In Geometry and analysis of fractals, Springer Proc. Math. Stat. vol. 88, pages 303–323 (Springer, Heidelberg, 2014).Google Scholar
Shmerkin, P.. On Furstenberg’s intersection conjecture, self-similar measures, and the L q norms of convolutions. Ann. of Math. (2), 189(2) (2019) 319–391.CrossRefGoogle Scholar
Shmerkin, P. and Suomala, V.. A class of random Cantor measures, with applications. In Recent developments in fractals and related fields, Trends Math., pages 233–260 (Birkhäuser/Springer, Cham, 2017).CrossRefGoogle Scholar
Shmerkin, P. and Suomala, V.. Spatially independent martingales, intersections, and applications. Mem. Amer. Math. Soc. 251(1195) (2018), v+102.Google Scholar
Shmerkin, P. and Suomala, V.. Patterns in random fractals. Amer. J. Math. 142(3) (2020), 683–749.CrossRefGoogle Scholar
Wu, M.. A proof of Furstenberg’s conjecture on the intersections of ×p- and ×q-invariant sets. Ann. of Math. (2) 189(3) (2019), 707–751.CrossRefGoogle Scholar
Zähle, U.. Random fractals generated by random cutouts. Math. Nachr. 116 (1984), 27–52.CrossRefGoogle Scholar