No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
§ 1. If the kinetic potential for the relative motion of two masses is written with an added constant as
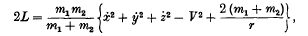
a close connexion with the relativity quadratic appears. The latter is in fact
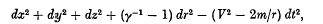
where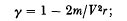 
a modification of the primary form
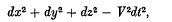
which shows an unaltered determinant. The condition in respect to the determinant, suggested, I believe, by Schwarzschild, is one which to me appears to give the most significant form to the results. From the dynamical standpoint we may regard it as imposing a counterpoise in the inertia coefficients to the modification introduced by the potential; or from a geometrical point of view we may regard it as minimizing the departure from the normal use of coordinates. An illuminating example of the loss of meaning that accompanies transformation in which this condition is disregarded is furnished by the isotropic form which is sometimes given to Einstein's quadratic.
* The need for recognition of change in all space variables is emphasized by M. Le Roux, as I see in a quotation from Comptes Rendus given by SirLarmor, Joseph, who also presses the same point, Proc. Camb. Phil. Soc., vol. xxi, pp. 415sqq.Google Scholar
* Proc. Camb. Phil. Soc., vol. xxii, Part 2, §17. There is a divisor h 2 affecting the gravitation constant, where h is the constant value of γd (Vt)/ds; in the above this is taken to be 1, or to be absorbed in the gravitation constant.Google Scholar