Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T07:49:04.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Primitive submodules for Drinfeld modules

Published online by Cambridge University Press:  30 June 2015

WENTANG KUO  and
DAVID TWEEDLE
WENTANG KUO
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada. e-mail: [email protected]
DAVID TWEEDLE
Affiliation:
Department of Mathematics and Statistics, University of The West Indies, St. Augustine, Trinidad and Tobago, West Indies. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The ring A = 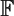$\mathbb{F}$r[T] and its fraction field k, where r is a power of a prime p, are considered as analogues of the integers and rational numbers respectively. Let K/k be a finite extension and let φ be a Drinfeld A-module over K of rank d and Γ ⊂ K be a finitely generated free A-submodule of K, the A-module structure coming from the action of φ. We consider the problem of determining the number of primes ℘ of K for which the reduction of Γ modulo ℘ is equal to 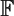$\mathbb{F}$℘ (the residue field of the prime ℘). We can show that there is a natural density of primes ℘ for which Γ mod ℘ is equal to 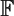$\mathbb{F}$℘. In certain cases, this density can be seen to be positive.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 2 , September 2015 , pp. 275 - 302
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Akbary, A. and Ghioca, D. Periods of orbits modulo primes. J. Number Theory. 129 (2009), no. 11, 2831–2842.Google Scholar
[2] Akbary, A., Ghioca, D. and Kumar Murty, V. Reductions of points on elliptic curves. Math. Ann. 347 (2010), no. 2, 365–394.Google Scholar
[3] Anderson, G. W. and Thakur, D. S. Tensor powers of the Carlitz module and zeta values. Ann. of Math. (2) 132 (1990), no. 1, 159–191.Google Scholar
[4] Bašmakov, M. I. Cohomology of Abelian varieties over a number field. Upsehi Mat. Nauk. 27 (1972), no. 6(168), 25–66.Google Scholar
[5] Chen, Y.-M. J. and Yu, J. On primitive points of elliptic curves with complex multiplication. J. Number Theory. 114 (2005), no. 1, 66–87.Google Scholar
[6] Drinfel'd, V. G. Elliptic modules. Mat. Sb. (N.S.) 94 (136) (1974), 594–627, 656.Google Scholar
[7] Fried, M. D. and Jarden, M. Field arithmetic (3rd edition). Ergeb. Math. Grenzeb. 3. Folge. A Series of Modern Surveys in Mathematics vol. 11 (Springer-Verlag, Berlin, 2008, Revised by Jarden).Google Scholar
[8] Gardeyn, F. Une borne pour l'action de l'inertie sauvage sur la torsion d'un module de Drinfeld. Arch. Math. (Basel) 79 (2002), no. 4, 241–251.Google Scholar
[9] Goss, D. Basic structures of function field arithmetic. Ergeb. Math. Grenzeb. (3) vol. 35 (Springer-Verlag, Berlin, 1996).Google Scholar
[10] Gupta, R. and Ram Murty, M. Primitive points on elliptic curves. Compositio Math. 58 (1986), no. 1, 13–44.Google Scholar
[11] Häberli, S. Kummer theory of Drinfeld modules. Master's thesis. Eidgenössiche Technische Hochschule Zürich (2011).Google Scholar
[12] Hall, C. and Voloch, J. F. Towards Lang–Trotter for elliptic curves over function fields. Pure Appl. Math. Q. 2 (2006), no. 1, 163–178.Google Scholar
[13] Hayes, D. Explicit class field theory in global function fields. In Studies in Algebra and Number Theory. Adv. in Math. Suppl. Stud. vol. 6 (Academic Press, New York, 1979), pp. 173–217.Google Scholar
[14] Hsu, C.-N. On Artin's conjecture for the Carlitz module. Compositio Math. 106 (1997), no. 3, 247–266.Google Scholar
[15] Hsu, C.-N. and Yu, J. On Artin's conjecture for rank one Drinfeld modules. J. Number Theory. 88 (2001), no. 1, 157–174.Google Scholar
[16] Lang, S. Algebra (3rd edition). Grad. Texts Math. vol. 211 (Springer-Verlag, New York, 2002).Google Scholar
[17] Lang, S. and Trotter, H. Primitive points on elliptic curves. Bull. Amer. Math. Soc. 83 (1997), no. 2, 289–292.Google Scholar
[18] Lang, S. and Weil, A. Number of points of varieties in finite fields. Amer. J. Math. 76 (1954), 819–827.Google Scholar
[19] Li, A. A note on Kummer theory of division points over singular Drinfeld modules. Bull. Austral. Math. Soc. 64 (2001), no. 1, 15–20.Google Scholar
[20] Pink, R. and Rütsche, E. Image of the group ring of the Galois representation associated to Drinfeld modules. J. Number Theory 129 (2009), no. 4, 866–881.Google Scholar
[21] Pink, R. Kummer theory for Drinfeld modules. arXiv preprint arXiv:1202.4732 (2012).Google Scholar
[22] Poonen, B. Local height functions and the Mordell–Weil theorem for Drinfel'd modules. Compositio Math. 97 (1995), no. 3, 349–368.Google Scholar
[23] Ribet, K. A. Dividing rational points on Abelian varieties of CM-type. Compositio Math. 33 (1976), no. 1, 69–74.Google Scholar
[24] Ribet, K. A. Kummer theory on extensions of abelian varieties by tori. Duke Math. J. 46 (1979), no. 4, 745–761.Google Scholar
[25] Rosen, M. Number theory in function fields. Grad. Texts Math. vol. 210 (Springer–Verlag, New York, 2002).Google Scholar
[26] Serre, J.-P. Local fields. Graduate Texts in Math. vol. 6 (Springer–Verlag, New York, 1979, Translated from the French by Marvin Jay Greenberg).Google Scholar