The postulation of a multiple curve
Published online by Cambridge University Press: 24 October 2008
Extract
1. The postulation of a multiple curve for primals of sufficiently large order in space of any number of dimensions has been obtained recently by J. A. Todd, by a simple and elegant degeneration argument which, however, is not deemed to be a conclusive proof by the author himself. And, indeed, in order to make sure of the unconditional validity of such an argument, one should ascertain whether
(i) the postulation θk of an irreducible non-singular curve ϲ, of order c and genus p, for the primals of sufficiently large order n of [r + 2] (r ≥ 1), required to go through it with multiplicity k (≥ 1), is a function of k, c, p, n, r only;
(ii) it is possible, by means of a continuous variation of ϲ, to reduce this curve to connected polygon ϲ′ having the same virtual characters as ϲ, in such a way that each intermediate position of ϲ is still irreducible and non-singular;
(iii) the postulation θk of ϲ equals the similarly defined postulation 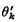 of ϲ′.
of ϲ′.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 38 , Issue 4 , November 1942 , pp. 368 - 377
- Copyright
- Copyright © Cambridge Philosophical Society 1942
References
REFERENCES
- 1
- Cited by


