No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
In this paper we continue the investigation of positive-moment problems, begun in (4). For an arbitrary index set A we consider a family (fα)α ∈ A of measurable real-valued functions on a measure-space (X, 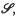 µ). We suppose throughout that
µ). We suppose throughout that
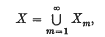
where (Xm) is an increasing sequence of measurable subsets of X and where, for each α in A and each m, fα is µ-integrable over Xm. Let (сα)α ∈ A be a given family of real numbers. We consider the following restricted positive-moment problem: does there exist a measurable function g on X such that 0 ≤° g ≤° 1 and such that
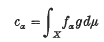
for every α in A? (Here the symbol ‘≤°’ indicates that the relation ≤ holds almost everywhere with respect to µ on X. Symbols ‘ = °, <°, …’ are used similarly.) If such a g exists we call (сα)α ∈ A a moment family for the problem: