Published online by Cambridge University Press: 24 October 2008
1. The present paper continues the investigation begun in (5). This earlier paper concluded with the description of a pencil P of canonical curves of genus 6 on a del Pezzo quintic surface F, but had first to describe the relevant features of the mapping of prime sections of F on a plane p by cubic curves circumscribing a quadrangle in p. It remains now to consider F and P in their ambient [5] in relation to G, the group, isomorphic to the symmetric group 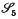 of degree 5, of self-projectivities of F.
of degree 5, of self-projectivities of F.