Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T11:20:08.745Z Has data issue: false hasContentIssue false
  • English
  • Français

Pair correlation for fractional parts of αn2

Published online by Cambridge University Press:  15 January 2010

D. R. HEATH–BROWN
D. R. HEATH–BROWN*
Affiliation:
Mathematical Institute, 24–29, St. Giles', Oxford, OX1 3LB. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

It was proved by Weyl [8] in 1916 that the sequence of values of αn2 is uniformly distributed modulo 1, for any fixed real irrational α. Indeed this result covered sequences αnd for any fixed positive integer exponent d. However Weyl's work leaves open a number of questions concerning the finer distribution of these sequences. It has been conjectured by Rudnick, Sarnak and Zaharescu [6] that the fractional parts of αn2 will have a Poisson distribution provided firstly that α is “Diophantine”, and secondly that if a/q is any convergent to α then the square-free part of q is q1+o(1). 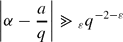Here one says that α is Diophantine if one has(1.1)for every rational number a/q and any fixed ϵ > 0. In particular every real irrational algebraic number is Diophantine. One would predict that there are Diophantine numbers α for which the sequence of convergents pn/qn contains infinitely many squares amongst the qn. If true, this would show that the second condition is independent of the first. Indeed one would expect to find such α with bounded partial quotients.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 148 , Issue 3 , May 2010 , pp. 385 - 407
Copyright
Copyright © Cambridge Philosophical Society 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Halberstam, H. and Richert, H.-E.Sieve Methods. London Mathematical Society Monographs, No. 4 (Academic Press, 1974).Google Scholar
[2]Heath–Brown, D. R.Diophantine approximation with square-free numbers. Math. Z. 187 (1984), 335–344.CrossRefGoogle Scholar
[3]Linnik, Yu.V. and Vinogradov, A. I.Estimate of the sum of the number of divisors in a short segment of an arithmetic progression. Uspehi Mat. Nauk (N.S.) 12 (1957), 4(76) 277–280.Google Scholar
[4]Marklof, J. and Strömbergsson, A.Equidistribution of Kronecker sequences along closed horocycles. Geom. Funct. Anal. 13 (2003), 1239–1280.CrossRefGoogle Scholar
[5]Rudnick, Z. and Sarnak, P.The pair correlation function of fractional parts of polynomials. Commun. Math. Phys. 194 (1998), 61–70.CrossRefGoogle Scholar
[6]Rudnick, Z., Sarnak, P. and Zaharescu, A.The distribution of spacings between the fractional parts of n 2α. Invent. Math. 145 (2001), 37–57.CrossRefGoogle Scholar
[7]Truelsen, J. On the pair correlation for the fractional parts of n 2α and a related problem, to appear.Google Scholar
[8]Weyl, H.Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77 (1916), 313–352.CrossRefGoogle Scholar