Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T08:37:40.866Z Has data issue: false hasContentIssue false
  • English
  • Français

The order-bound topology on Riesz spaces

Published online by Cambridge University Press:  24 October 2008

Yau-Chuen Wong
Yau-Chuen Wong
Affiliation:
United College, The Chinese University of Hong Kong, Hong Kong
Get access Rights & Permissions [Opens in a new window]

Extract

1. Introduction. Let (X, C) be a Riesz space (or vector lattice) with positive cone C. A subset B of X is said to be solid if it follows from |x| ≤ |b| with b in B that x is in B (where |x| denotes the supremum of x and − x). The solid hull of B (absolute envelope of B in the terminology of Roberts (2)) is denoted to be the smallest solid set containing B, and is denoted by SB. A locally convex Hausdorff topology 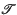on (X, C) is called a locally solid topology if 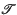admits a neighbourhood-base of 0 consisting of solid and convex sets in X; and (X, C, 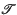), where 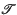is a locally solid topology, is called a locally convex Riesz space.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 3 , May 1970 , pp. 587 - 593
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Namioka, I.Partially ordered linear topological spaces. Mem. Amer. Math. Soc. 24 (1957).Google Scholar
(2)Roberts, G. T.Topologies in vector lattices. Proc. Cambridge Philos. Soc. 48 (1952), 533–46.CrossRefGoogle Scholar
(3)Schaefer, H. H.Topological vector spaces (Macmillan, New York, 1966).Google Scholar
(4)Yua-Chuen, Wong. Locally o-convex Riesz spaces. Proc. London Math. Soc. (3), 19 (1969), 289–309.Google Scholar
(5)Yau-Chuen, Wong. Order-infrabarrelled Riesz spaces. Math. Ann. 183 (1969), 17–32.Google Scholar