Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T08:48:15.880Z Has data issue: false hasContentIssue false
  • English
  • Français

On Toeplitz sections in sequence spaces

Published online by Cambridge University Press:  24 October 2008

Martin Buntinas
Martin Buntinas
Affiliation:
Loyola University of Chicago
Get access Rights & Permissions [Opens in a new window]

Extract

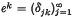The concept of sectional convergence (AK) in FK-spaces was investigated by Zeller in (20). In (5) and (6), Garling investigated convergent and bounded sections in more general topological sequence spaces. Many of the results hold for Toeplitz sections in sequence spaces. A topological sequence space has the property of Toeplitz sectional convergence (TK) if and only if the unit sequences form a Toeplitz basis. In section 3, we present characterizations of Toeplitz sectional boundedness (TB) and functional Toeplitz sectional convergence (FTK) in terms of βT- and γT-duality. In section 4, we apply our results to summability fields. These results are related to the Hardy-Bohr property of multipliers for Cesàro summable sequences of positive order. In section 5, we characterize the properties TK and TB in FK-spaces by factorization statements.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 3 , November 1975 , pp. 451 - 460
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Andersen, A. F.On the extension within the theory of Cesàro summability of a classical convergence theorem of Dedekind. Proc. London Math. Soc. (3) 8 (1958), 1–52.CrossRefGoogle Scholar
(2)Bosanquet, L. S.Note on convergence and summability factors (III). Proc. London Math. Soc. (2) 50 (1949), 482–496.Google Scholar
(3)Buntinas, M.Convergent and bounded Cesàro sections in FK-Spaces. Math. Z. 121 (1971), 191–200.CrossRefGoogle Scholar
(4)Buntinas, M.On sectionally dense summability fields. Math. Z. 132 (1973), 141–149.CrossRefGoogle Scholar
(5)Garling, D. J. H.On topological sequence spaces. Proc. Cambridge Philos. Soc. 63 (1967), 997–1019.Google Scholar
(6)Garling, D. J. H.The β- and γ-duality of sequence spaces. Proc. Cambridge Philos. Soc. 63 (1967), 963–981.CrossRefGoogle Scholar
(7)Goes, G.Complementary spaces of Fourier coefficients, convolutions, and generalized matrix transformations and operators between BK-spaces. J. Math. Mech. 10 (1961), 135–158.Google Scholar
(8)Goes, G.Topics in topological sequence spaces. Manuscript of a course given at Illinois Institute of Technology (Chicago, 1972).Google Scholar
(9)Goes, G.Summen von FK-Räumen, Funktionale Abschnittskonvergenz und Umkehrsätze. Tôhoku Math. J. 26 (1974), 487–504.CrossRefGoogle Scholar
(10)Jurkat, W. and Peyerimhoff, A.Über Sätze vom Bohr-Hardy'schen Typ. Tôhoku Math. J. 17 (1965), 55–71.CrossRefGoogle Scholar
(11)Kurtz, J. C.Multipliers on some sequence spaces. Proc. Cambridge Philos. Soc. 72 (1972), 393–401.CrossRefGoogle Scholar
(12)Marti, J. T.Introduction to the theory of bases (New York, 1969).CrossRefGoogle Scholar
(13)Meyers, G.On Toeplitz sections in FK-spaces. Studia Math. (to appear).Google Scholar
(14)Peterson, G. E.Summability factors. Proc. London Math. Soc. (3) 19 (1969), 341–356.Google Scholar
(15)Ruckle, W. H.An abstract concept of the sum of a numerical series. Canal. J. Math. 22 (1970), 863–874.Google Scholar
(16)Schaefer, H. H.Topological vector spaces (New York, 1966).Google Scholar
(17)Summers, W. H.Factorization in Fréchet spaces. Studia Math. 39 (1971), 209–216.CrossRefGoogle Scholar
(18)Wilansky, A.Functional analysis (New York, 1964).Google Scholar
(19)Zeller, K.Allgemeine Eigenschaften von Limitierungsverfahren. Math. Z. 53 (1951), 463–487.CrossRefGoogle Scholar
(20)Zeller, K.Abschnittskonvergenz in FK-Räumen. Math. Z. 55 (1951), 55–70.Google Scholar
(21)Zeller, K.Approximation in Wirkfeldern von Summierungsverfahren. Arch. Math. 4 (1953), 425–431.CrossRefGoogle Scholar