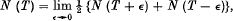
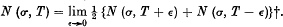
† These equations are, of course, then valid for all T.

‡ We adhere strictly, however, to the condition β > σ for the real part of a zero counted in N (σ, T). A halving convention here has something against it and nothing in its favour.

§ Backlund, R., Acta Mathematica, 41 (1918), 345–375CrossRefGoogle Scholar. With our conventions the results are evidently true for all T if true for “wurzelfrei” T.

* Thus we write, e.g. (sin θ + 2)³ < (A + A)^a < A.

† f(x) = O {ø (x)} means | f(x)/ø(x) | < K (x > x ₀): an O involves two constants, K and x ₀. Our convention is that both are A's.

* See Hardy, G. H. and Littlewood, J. E., Proc. London Math. Soc. (2), 21 (1921), 39–74.Google Scholar

† Loc. cit., 53.

* Bohr, H., Landau, E., and Littlewood, J. E., Bull. Acad. Belgique, 15 (1913), 1144–1175, 1166.Google Scholar

* It is easily verified that exists: in fact near a singularity σ₀ + it ₀ of ø′/ø we have

and the integral of this with respect to σ converges. We may invert the order of integration and ignore lines on which the inner integrals do not exist.

* Since f = O (2^−σ) (σ ≥ 2), so that

* If σ₁ > 1 the result is trivial. If not, then and

† Carlson, F., Arkiv för Mat., Ast. och Fys., 15 (1920), No. 20Google Scholar. The details of the proof can be lightened by Theorem 2, which enables us to reduce the double integration to a single one. Carlson's theorem lies much deeper than ours for fixed σ, but it appears to throw no light on the present problem.

‡ Cramér, H., Math. Zeitschr., 4 (1919), 104–130, 122–130CrossRefGoogle Scholar, proves, by an entirely different method, that

* Backlund, R., Öfversigt Finska Vetensk. Soc., 61 (1918–1919), No. 9.Google Scholar

† o's are not uniform in δ. O's (by our current convention) are absolute, and so uniform in δ. We must therefore bear in mind that, e.g., a o (log T) is not necessarily of the form O (log T); for example δ⁻¹ is of the first form but not of the second.

‡ Landau, E., Handbuch, p. 337Google Scholar. We refer to this treatise as H. B.

§ H.B., pp. 316–318.

‖ H.B., p. 339.

* Math. Zeitschr., 2 (1918), 237–241.Google Scholar

* Results intermediate between this and the S (T) = O (log T) which is true without the Riemann hypothesis have been given by Bohr, Cramér, and Landau.

* The O's here are naturally not absolute.

† See Hardy, G. H. and Littlewood, J. E., Proc. London Math. Soc. (2), 11 (1913)Google Scholar. If R (T) is continuous the theorem is a case of Theorem 6 (a), with

In the actual case we can modify R (T) in a small neighbourhood of each discontinuity so as to make it continuous, altering R ₁ (T), R ₂ (T) by arbitrarily little.

* Lindelöf, E., Acta Soc. Scient. Fenn., 46 (1915)Google Scholar.

* This part of the argument is one of the main keys to the proof of Theorem 11.

* H. B., p. 316.

* The modifications necessary if a _n < 0 or a _n+2 = − ∞ can be supplied by the reader. Since actually a _n > 0 it is not worth while to set out the details.