Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T07:49:29.652Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Stability of the Periodic States of the Triode Oscillator

Published online by Cambridge University Press:  24 October 2008

W. M. H. Greaves
W. M. H. Greaves
Affiliation:
St John's College
Get access Rights & Permissions [Opens in a new window]

Extract

1. Appleton and van der Pol have shown that in a simple Triode or Dynatron generating circuit the anode potential v is related to the time t by a differential equatior of the type

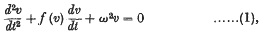
where f (v) is a power series in v, and may be written

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 1 , February 1924 , pp. 16 - 23
Copyright
Copyright © Cambridge Philosophical Society 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

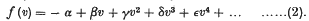
* Phil. Mag., Ser. 6, Vol. 43, No. 253, p. 179, 01 1922.Google Scholar

† Phil. Mag., Ser. 6, Vol. 45, No. 267; p. 402, 03 1923.Google Scholar

‡ Phil. Mag., Vol. 45, pp. 401–414, 03 1923.CrossRefGoogle Scholar

§ Proc. Roy. Soc., A., Vol. 103, pp. 516–524, 1923.CrossRefGoogle Scholar

∥ This possibility is not definitely excluded by the first investigation of Appleton and van der Pol, which was intended purely as a first approximation and in which a whole series of periodic terms is neglected.

* For details of this transformation see Proc. Roy. Soc., A., Vol. 103, p. 517, 1923.Google Scholar

* It was explained in one of the previous papers (Proc. Roy. Soc., A, Vol. 103, p. 517, 1923) that a solution of an equation such as (8) is to be regarded as periodic if at the end of each period x resumes its original value and y changes by a multiple of 2π. Such a solution will be strictly periodic when expressed in terms of the original dependent variable v.Google Scholar

† The actual details of the reversion are not needed here. It may be carried out if desired with the aid of Lagrange's formula. (See, for instance, Goursat, , Cours d'Analyse, t. 1, ch. IX, p. 481.)Google Scholar

* See note at end of paper.

* Strictly speaking we have only proved so far that (when c > 0) the periodic solution of (13) corresponding to x=a is stable and we have not proved the stability of the corresponding group of solutions of (8). This, however, will be proved in the following section.

* Loc. cit., equation (10), p. 182.Google Scholar

* This method of approximation is that which ie used in celestial mechanics for the purpose of calculating the secular motions of the major planets. cf.Tisserand, , Mécanique Céleste, t. I, ch. XXVI.Google Scholar

† Cf. Charlier, , Mechanik des Himmels, vol. 1, p. 89,Google Scholar or the original source, Weierstrass, , Ges. Werke, Bd. 11, p. 1.Google Scholar

* Cf. Poincaré, , Lea méthodes nouvelles de la mécanique céleste, t. I, ch. VII, pp. 335 et seq.Google Scholar