Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-10T16:09:22.287Z Has data issue: false hasContentIssue false
  • English
  • Français

On the set of zero coefficients of a function satisfying a linear differential equation

Published online by Cambridge University Press:  22 February 2012

JASON P. BELL ,
STANLEY N. BURRIS  and
KAREN YEATS
JASON P. BELL
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Dr., Burnaby, BC, V5A 1S6Canada. e-mail: [email protected]
STANLEY N. BURRIS
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1, Canada. e-mail: [email protected]
KAREN YEATS
Affiliation:
Department of Mathematics, Simon Fraser University, 8888 University Dr., Burnaby, BC, V5A 1S6, Canada. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be a field of characteristic zero and suppose that f: 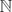→ K satisfies a recurrence of the form

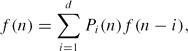\[f(n) = \sum_{i=1}^d P_i(n) f(n-i),\]
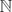for n sufficiently large, where P1(z),. . .,Pd(z) are polynomials in K[z]. Given that Pd(z) is a nonzero constant polynomial, we show that the set of n ∈ for which f(n) = 0 is a union of finitely many arithmetic progressions and a finite set. This generalizes the Skolem–Mahler–Lech theorem, which assumes that f(n) satisfies a linear recurrence. We discuss examples and connections to the set of zero coefficients of a power series satisfying a homogeneous linear differential equation with rational function coefficients.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 153 , Issue 2 , September 2012 , pp. 235 - 247
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adamczewski, B. and Bell, J. P.On the set of zero coefficients of algebraic power series. Invent. Math. 187, no. 2 (2012), 343–393.CrossRefGoogle Scholar
[2]Allouche, J.-P. and Shallit, J.Automatic Sequences. Theory, Applications, Generalizations (Cambridge University Press, 2003).CrossRefGoogle Scholar
[3]Bell, J. P.A generalised Skolem–Mahler–Lech Theorem for affine varieties. J. London Math. Soc. 73 (2006), 367–379.CrossRefGoogle Scholar
[4]Bell, J. P.Corrigendum to “A generalised Skolem–Mahler–Lech Theorem for affine varieties”. J. London Math. Soc. 78 (2008), 267–272.CrossRefGoogle Scholar
[5]Bell, J. P., Burris, S. N. and Yeats, K.Spectra and Systems of Equations. arXiv:0911.2494.Google Scholar
[6]Bell, J. P., Ghioca, D. and Tucker, T. J.The dynamical Mordell–Lang problem for étale maps. Amer. J. Math. 132, no. 6 (2010), 1655–1675.CrossRefGoogle Scholar
[7]Bézivin, J.-P.Une généralisation du théorème de Skolem–Mahler–Lech. Quart. J. Math. Oxford Ser. (2). 40 (1989), no. 158, 133–138.CrossRefGoogle Scholar
[8]Bézivin, J.-P. and Laohakosol, V.On the theorem of Skolem–Mahler–Lech. Exposition. Math. 9 (1991), no. 1, 89–96.Google Scholar
[9]Bousquet–Mélou, M.Walks in the quarter plane: Kreweras' algebraic model. Ann. Appl. Probab. 15 (2005), no. 2, 1451–1491.CrossRefGoogle Scholar
[10]Chyzak, F. and Salvy, B.Non-commutative elimination in Ore algebras proves multivariate identities. J. Symbolic Comput. 26 (1998), no. 2, 187–227.CrossRefGoogle Scholar
[11]Chyzak, F., Mishna, M. and Bruno, B. SalvyEffective scalar products of D-finite symmetric functions. J. Combin. Theory Ser. A 112 (2005), no. 1, 1–43.CrossRefGoogle Scholar
[12]Derksen, H.A Skolem–Mahler–Lech theorem in positive characteristic and finite automata. Invent. Math. 168 (2007), 175–224.CrossRefGoogle Scholar
[13]Everest, G., van der Poorten, A., Shparlinski, Alf I. and Ward, T.Recurrence sequences. Mathematical Surveys and Monographs, 104 (Amer. Math. Soc. 2003).CrossRefGoogle Scholar
[14]Evertse, J.–H., Schlickewei, H. P. and Schmidt, W. M.Linear equations in variables which lie in a multiplicative group. Ann. of Math. (2) 155 (2002), no. 3, 807–836.CrossRefGoogle Scholar
[15]Garoufalidis, S.G-functions and multisum versus holonomic sequences. Adv. Math. 220 (2009), no. 6, 19451955.CrossRefGoogle Scholar
[16]Gessel, I.Symmetric functions and P-recursiveness. J. Combin. Theory Ser. A 53 (1990), no. 2, 257–285.CrossRefGoogle Scholar
[17]Hansel, G.Une démonstration simple du théorème de Skolem–Mahler–Lech. Theoret. Comput. Sci. 43 (1986), no. 1, 91–98.CrossRefGoogle Scholar
[18]Lang, S.Algebraic number theory. Second edition. Graduate Texts in Mathematics, 110 (Springer-Verlag, 1994).CrossRefGoogle Scholar
[19]Laohakosol, V.Some extensions of the Skolem–Mahler–Lech theorem. Exposition. Math. 7 (1989), no. 2, 137–187.Google Scholar
[20]Lech, C.A note on recurring series. Ark. Mat. 2 (1953), 417–421.CrossRefGoogle Scholar
[21]Li, H. and Van Oystaeyen, F.Elimination of variables in linear solvable polynomial algebras and ∂-holonomicity. J. Algebra 234 (2000), no. 1, 101–127.Google Scholar
[22]Mahler, K.Eine arithmetische Eigenshaft der Taylor–Koeffizienten rationaler Funktionen. Proc. Kon. Nederlandsche Akad. v. Wetenschappen 38 (1935), 50–60.Google Scholar
[23]Mahler, K.On the Taylor coefficients of rational functions. Proc. Camb. Phil. Soc. 52 (1956), 39–48.CrossRefGoogle Scholar
[24]Mahler, K.Addendum to the paper “On the Taylor coefficients of rational functions". Proc. Camb. Phil. Soc. 53 (1957), 544.CrossRefGoogle Scholar
[25]Mahler, K.p-adic Numbers and Their Functions, Second ed. (Cambridge University Press, Cambridge, New York, 1981).Google Scholar
[26]Methfessel, C.On the zeros of recurrence sequences with non-constant coefficients. Arch. Math. (Basel) 74 (2000), no. 3, 201–206.CrossRefGoogle Scholar
[27]van der Poorten, A. J.A proof that Euler missed . . . Apéry's proof of the irrationality of ζ(3). Math. Intelligencer 1 (1979), 195–203.CrossRefGoogle Scholar
[28]van der Poorten, A. J.Some facts that should be better known; especially about rational functions. Number Theory and Applications ed. Mollin, Richard A., (NATO–Advanced Study Institute, Banff, 1988), (Kluwer Academic Publishers, 1989), 497–528.Google Scholar
[29]van der Poorten, A. J. and Tijdeman, R.On common zeros of exponential polynomials. Enseign. Math. (2) 21 (1975), no. 1, 57–67.Google Scholar
[30]Robert, A.A course in p-adic analysis. Graduate Texts in Mathematics, 198 (Springer-Verlag, 2000).CrossRefGoogle Scholar
[31]Rubel, L. A.Some research problems about algebraic differential equations. Trans. Amer. Math. Soc. 280 (1983), no. 1, 43–52 (Problem 16).CrossRefGoogle Scholar
[32]Skolem, T. Ein Verfahren zur Behandlung gewisser exponentialer Gleichungen und diophantischer Gleichungen. C. r. 8 Congr. Scand. à Stockholm (1934), 163–188.Google Scholar
[33]Stanley, R.Differentiably finite power series. European J. Combin. 1 (1980), 175–188.CrossRefGoogle Scholar
[34]Strassman, R.Über den Wertevorrat von Potenzreihen im Gebiet der p-adischen Zahlen. J. Reine Angew. Math. 159 (1928), 13–28; 65–66.CrossRefGoogle Scholar
[35]Wilf, H. S. and Zeilberger, D.An algorithmic proof theory for hypergeometric (ordinary and “q”) multisum/integral identities. Invent. Math. 108 (1992), no. 3, 575–633.CrossRefGoogle Scholar