Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-29T19:39:11.421Z Has data issue: false hasContentIssue false
  • English
  • Français

On the product of three non-homogeneous linear forms

Published online by Cambridge University Press:  24 October 2008

H. Davenport
H. Davenport
Affiliation:
University CollegeLondon
Get access Rights & Permissions [Opens in a new window]

Extract

Let ξ, η, ζ be linear forms in u, v, w with real coefficients and determinant Δ ≠ 0. A conjecture of Minkowski, which was subsequently proved by Remak, tells us that for any real numbers a, b, c there exist integral values of u, v, w for which

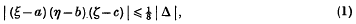
and the constant ⅛ on the right is best possible.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 43 , Issue 2 , April 1947 , pp. 137 - 152
Copyright
Copyright © Cambridge Philosophical Society 1947

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* J. London Math. Soc. 14 (1939), 47–51.Google Scholar

† When making this suggestion, Prof. Mordell told me that he had proved (3) for the linear forms (4) with a value of appreciably less than ⅛.

* See Davenport, , Proc. Cambridge Phil. Soc. 39 (1942), 1–21CrossRefGoogle Scholar and references given there.

† Proc. K. Akad. Wet. Amsterdam, 49 (1946), 815–821.Google Scholar

* The field k(θ) is, of course, galoisian, and is transformed into itself by θ → ø, which implies ø → ψ and ψ → θ.

† We name θ ø, ψ so that

* See the previous footnote.

* This field has the same properties as those stated for k(θ) in an earlier footnote.

† We name θ′ ø′, ψ′ so that