Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T07:26:30.079Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Parseval formulae for Fourier transforms

Published online by Cambridge University Press:  24 October 2008

Sheila M. Edmonds
Sheila M. Edmonds
Affiliation:
Newnham CollegeCambridge Communicated by G. H. Hardy
Get access Rights & Permissions [Opens in a new window]

Extract

1. The object of this paper is to discuss conditions of validity of the Parseval formulae for Fourier integrals:

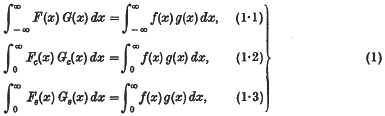
where the transforms are defined by ordinary convergence; we shall not be concerned with the more elegant theory in which they are given by convergence in mean.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 38 , Issue 1 , January 1942 , pp. 1 - 19
Copyright
Copyright © Cambridge Philosophical Society 1942

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* I.e. the infinite integrals being taken in the Lebesgue or Cauchy sense. The notation will be used for the Cauchy integral similarly for etc.

† Titchmarsh, E. C., Introduction to the theory of Fourier integrals (Oxford, 1937), 54Google Scholar. The use of small and capital letters eliminates the ambiguity of the term ‘Fourier transform’.

* These conditions will be referred to below as ‘conditions (A)’.

* [ ] denoting ‘greatest integer contained in’.

* This inequality is proved, as in Theorem 38, by writing g(t, x) in the form

* Hardy, and Titchmarsh, , ‘A note on Parseval's theorem for Fourier transforms’, J. London Math. Soc. 6 (1931), 44–8 (47)CrossRefGoogle Scholar. The theorem is Theorem 70 of Prof. Titchmarsh's book.

† In the wide sense (‘decreasing’ will be used in this sense throughout the proof). Actually the result is true in the strict sense, but we shall not require to use this fact.

* If f(x), g(x) have continuous derivatives for x > 0, a more obvious way of proving this is to write the integral concerned in the form

and calculate its derivative by differentiating under the integral sign. The method can be adapted to deal with the general case.

* Proof as in Titchmarsh, op. cit., Theorem 6, for example.

* See Titchmarsh, op. cit., Theorem 123.