Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T07:36:49.210Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Lines which meet Four Regions* in Hyper-Space

Published online by Cambridge University Press:  24 October 2008

R. Vaidyanathaswamy
R. Vaidyanathaswamy
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

The problem of finding the number of r-dimensional regions which are situated in a space Sn of n dimensions, and which satisfy a suitable number of conditions of certain assigned types (called “ground-conditions”) has been investigated by Schubert. A special class of such problems arises when the r-dimensional region is merely required to intersect k regions Pλ of rλ dimensions (λ = 1, 2 … k) situated in general position in Sn where for the finiteness of the sought number we must have

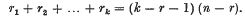
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 22 , Issue 1 , February 1924 , pp. 49 - 53
Copyright
Copyright © Cambridge Philosophical Society 1924

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† Math. Annalen, Bd. 26, 38.

‡ For an account of this principle see Schubert, Kalkul der Abzahlenden Geometric, or preferably Zeuthen, “Abzahlenden Methoden” (Ency. Math. Wiss.).

§ Math. Annalen, Bd. 59.