Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Haeusler, Erich
and
Mason, David M.
1987.
Laws of the iterated logarithm for sums of the middle portion of the sample.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 101,
Issue. 2,
p.
301.
Griffin, Philip S.
and
Pruitt, William E.
1987.
The central limit problem for trimmed sums.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 102,
Issue. 2,
p.
329.
Griffin, Philip S.
1988.
The influence of extremes on the law of the iterated logarithm.
Probability Theory and Related Fields,
Vol. 77,
Issue. 2,
p.
241.
Maller, R.A.
1990.
Defining extremes and trimming by minimum covering sets.
Stochastic Processes and their Applications,
Vol. 35,
Issue. 1,
p.
169.
Hahn, Marjorie G.
Kuelbs, Jim
and
Weiner, Daniel C.
1990.
The asymptotic distribution of magnitude-Winsorized sums via self-normalization.
Journal of Theoretical Probability,
Vol. 3,
Issue. 1,
p.
137.
Csörgő, Sándor
Haeusler, Erich
and
Mason, David M.
1991.
Sums, Trimmed Sums and Extremes.
p.
215.
Hahn, Marjorie G.
Kuelbs, Jim
and
Weiner, Daniel C.
1991.
Sums, Trimmed Sums and Extremes.
p.
1.
Griffin, Philip S.
and
Pruitt, William E.
1991.
Sums, Trimmed Sums and Extremes.
p.
55.
Griffin, Philip S.
and
Mason, David M.
1991.
On the asymptotic normality of self-normalized sums.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 109,
Issue. 3,
p.
597.
Maller, R. A.
1991.
Sums, Trimmed Sums and Extremes.
p.
179.
Whalen, Edward
1992.
The asymptotic distribution of magnitude trimmed sums for distributions in the Feller class.
Journal of Theoretical Probability,
Vol. 5,
Issue. 3,
p.
447.
Hahn, Marjorie G.
and
Weiner, Daniel C.
1992.
Asymptotic behavior of self-normalized trimmed sums: Nonnormal limits II.
Journal of Theoretical Probability,
Vol. 5,
Issue. 1,
p.
169.
Kesten, Harry
1993.
Convergence in distribution of lightly trimmed and untrimmed sums are equivalent.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 3,
p.
615.
Maejima, Makoto
1993.
Trimmed sums of i.i.d. Banach space valued random variables.
Journal of Theoretical Probability,
Vol. 6,
Issue. 1,
p.
57.
Kesten, Harry
and
Maller, R.A.
1997.
Random Deletion Does Not Affect Asymptotic Normality or Quadratic Negligibility.
Journal of Multivariate Analysis,
Vol. 63,
Issue. 1,
p.
136.
Griffin, P. S.
and
Maller, R. A.
1999.
Perplexing Problems in Probability.
p.
219.
Griffin, Philip S.
and
Qazi, Fozia S.
2002.
Limit laws of modulus trimmed sums.
The Annals of Probability,
Vol. 30,
Issue. 3,
Berkes, István
Horváth, Lajos
and
Schauer, Johannes
2011.
Asymptotics of trimmed CUSUM statistics.
Bernoulli,
Vol. 17,
Issue. 4,
BERKES, ISTVÁN
HORVÁTH, LAJOS
and
SCHAUER, JOHANNES
2012.
ASYMPTOTIC BEHAVIOR OF TRIMMED SUMS.
Stochastics and Dynamics,
Vol. 12,
Issue. 01,
p.
1150002.
Berkes, István
and
Horváth, Lajos
2012.
The central limit theorem for sums of trimmed variables with heavy tails.
Stochastic Processes and their Applications,
Vol. 122,
Issue. 2,
p.
449.


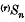 be
be 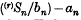 coverages in distribution to
coverages in distribution to 