1. The questions considered in this note are suggested by the elementary topology of the trajectories of systems of non-linear differential equations. Such a system may be assumed in the form

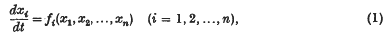
and the values of the dependent variables x1, x2, …, xn at ‘time’ t can be represented by a point P(t) in a ‘phase space’ 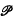. As t varies, P(t) describes a curve in 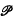, which is a trajectory of (1). Now it often happens that 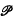contains a subspace E (usually of lower dimension) with the following properties: (i) by considering the trajectories generated by points P(t) which are, for t = 0, in E, all the trajectories of (1) are obtained; (ii) if P(0) is in E, then P(t) is not in E for 0 < t < c, where c is a constant independent of P(0) in E; (iii) if P(0) is in E, then the trajectory meets E again for some finite t at a point P(T) (T is not necessarily the same for all points of E). By considering P(T) as the image of P(O), a mapping of E into itself is defined which is associated with the system (1), and the topology of the trajectories of (1) can be studied conveniently by discussing this mapping. When the functions fi in (1) satisfy the continuity and Lipschitz conditions of the classical existence-and-uniqueness theorem, the mapping is one-one and continuous. The study of this ‘transformation theory’, initiated by Poincaré, has been developed chiefly by G. D. Birkhoff(l,2). His results have been applied to problems of ‘non-linear mechanics’ by N. Levinson(3).